Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.

Рассмотрим б.д.р. задачи P. ПустьB – его базисная матрица, а N, соответственно, небазисная матрица. Обозначим через П гиперплоскость, натянутую на расширенные вектора базиса , и проходящую через начало координат. Эта гиперплоскость однозначно определяется бази-сом B и ее направляющий вектор есть решение следующей системы урав-нений следовательно, . Оценки замещения симплекс-таблицы, соответствующей б.д.р. , образуют вектор . 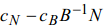Таким образом, если на первом шаге итерации симплекс-таблица, соответствующая б.д.р. , является двойственно допустимой, тоесть , то вектор y является допустимым решением двойственной задачи, тогда и – оптимальные решения. Их геометрическая интерпретация содержится в предыдущем параграфе. Если существует номер s такой, что , то это означает, что недопустимое решение двойственной задачи, то есть симплекс-таблица не двойственно допустима, а неоптимальное решение. Геометрически это эквивалентно тому, что вектор расположен ниже гиперплоскости П. Рассмотрим конус , натянутый на вектора :

. Если коэффициенты замещения , то множество 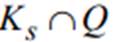содержит луч, исходящий из точки . Это следует из существования параметрического семейства векторов , которое использовалось при обосновании симплекс-метода. В этом случае задача (1)-(3) не имеет оптимального решения. Заметим, что это возможно тогда и только тогда, когда конус содержит полуось . Если конус не содержит полуось , то тогда 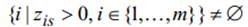и множество является отрезком, который в вырожденном случае может оказаться точкой. Если задача (1)-(3) невырож-денная,то отрезок отличен от точки. Его крайняя верхняя точка является образом базисного допустимого решения и лежит на грани образованной векторами , так как 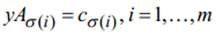. Это означает, что эта грань есть пересечение конуса с гиперплоскостью П. Тогда нижняя точка отрезка является геометрическим образом нового базисного допустимого решения и лежит на грани, порожденной векторами другими словами, 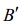– новый базис, образованный векторами . Точки пересечения конуса и прямой Q являются геометрическими образами решений, полученных из базисно допустимого решения x элементарным преобразованием, которое определяется вектором .

Не нашли, что искали? Воспользуйтесь поиском: