Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования

Рассмотрим задачу минимизации нелинейной ф-ции на параллелепипеде где Считаем, что целевая функция f удволетворяет условию Липшица с константой L = const > 0: Из этого следует, что f – непрерывная функция, следовательно, достигает своего минимального значения f* на параллелепипеде. Выберем на отрезке оси j следующие точки где h =2ε /L – шаг сетки, mj – нат. Число, удовлетворяющее неравенству 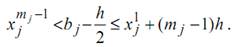На параллелепипеде Q введем сетку где j координата точки принимает одно из следующих зхначений . Пусть . Теорема: Для любой функции f(x) удовлетворящей уловию Липшица справедлива оценка

Множество является гиперкубом, рассмотрим произвольный гиперкуб из теоремы следует, что для любого верно Функцию выбора наилучшего решения определим на гиперкубах, которые являются атомарными множествами со стороной . Подмножества решений будем задавать в виде набора гиперкубов. На первом шаге имеем , где рекорд -- является центром гиперкуба со стороной .Пусть к следующему шагу есть разбиение и рекорд , проверяем элементы разбиения на наличие решения со значением лучше рекорда. Он считается проверенным и отбрасывается если выполнено одно из сл. условий

1. 2. Стороны гиперкуба Hl не превосходят величины 2ε/L. Если отброшены все элементы разбиения, то алгоритм закончил работу, если не все отброшены то выбираем следующее подмножество и проверяем и т. Д.

Не нашли, что искали? Воспользуйтесь поиском: