Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций

Представленный ниже алгоритм предназначается для поиска экстремума при наличии ограничений только типа неравенств. Рассмотрим задачу

Опишем в общем виде идею метода штрафов, используемого для решения следующей задачи (1)-(3). Рассмотрим функцию h: R ->R вида:

Определим функцию штрафа Очевидно, что

Следовательно, решение задачи (1)-(3) эквивалентно решению следующей задачи без ограничений

Основной недостаток этого подхода связан с разрывностью функции штрафа H, так как минимизация функции g в этом случае является весьма непростой задачей.

Основной недостаток метода внешних штрафов заключается в том, что оптимум x * аппроксимируется снаружи, то есть приближения x ₁, x ₂,…, x_l, полученные при коэффициентах штрафа k ₁, k ₂,…, k_l, не принадлежат множеству допустимых решений задачи, что и послужило причиной создания других методов штрафа, в которых оптимум аппроксимируется изнутри. Этим обосновывается их название – методы внутренних штрафов.

Определение 2. Функция B (x) называется барьерной функцией для Q, если B (x) определена и конечна на Int Q, B (x)>=0 и .

Примеры барьерных функций:

Определим штрафную функцию P_k (x) = a_kB (x), где a_k – коэффициент штрафа или барьерный коэффициент. Тогда решение задачи (1)-(3) сводится к решению последовательности задач минимизации вида

(24)

Предполагается, что a_k ->0 при k ->∞. Как и выше, считаем, что существует метод нахождения оптимального решения задачи (24). Пусть x_k = x (k) – оптимальное решение задачи (24) со значением барьерного коэффициента a_k. На практике для решения задачи (24) можно использовать метод градиентов. При этом, если Int Q ≠ и начальное приближение x ⁰ Int Q, то можно гарантировать, что все последующие приближения будут принадлежать Int Q. Действительно, рассмотрим итерационную формулу . Если в ней текущее приближение x_k Int Q, то при достаточно малой длине шага a _k новое приближение x^{k +1} Int Q.

Рассмотрим итерационный алгоритм. Пусть x^k Int Q – решение задачи (24) на шаге k.

Шаг k + 1. Находим решение задачи (24) со значением барьерного коэффициента a_{k +1} < a_k. Текущее решение x^k используется в качестве начального приближения. Если , то алгоритм завершает работу. Иначе перейти на следующий шаг.

С практической точки зрения важно, чтобы приближения, которые генерируются в процессе работы алгоритма, сходились к оптимальному решению задачи. Как и в предыдущем случае, возьмем = 0. Тогда алгоритм порождает бесконечную последовательность приближений. Оказывается, что при достаточно простых предположениях можно гарантировать сходимость этой последовательности к оптимуму.

Предположим, что задача (24) при любом k N достигает минимума на Q и для его вычисления используется один из итерационных методов безусловной оптимизации. Тогда, если начальное приближение x ⁰ Int Q, то из свойств барьерной функции следует, что данный алгоритм будет сходится к некоторому значению из множества IntQ. При доказательстве теоремы 6 предполагаем, что множество допустимых решений замкнуто, Int Q ≠ , f C ⁰(Rⁿ), B C ⁰ (IntQ), B (x) >= 0, x Int Q и, наконец, для любого элемента x Q существует последовательность { y_k } _{k N} , y_k Int Q, такая, что .

Теорема 6. Пусть выполняется одно из условий:

a) f (x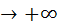_k) при k 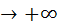для любой последовательности такой, что || x_k || при k ,

б) множество Q ограничено.

Тогда

1) последовательность имеет хотя бы одну предельную точку и любая предельная точка этой последовательности является оптимальным решением,

2) 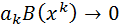при k .

Не нашли, что искали? Воспользуйтесь поиском: