Численные методы условной оптимизации. Метод ветвей и границ

Рассмотрим задачу Допустим, что множество допустимых решений Q является конечным, тогда одним из алгоритмов решения этой задачи является полный перебор, когда наилучшее найденное решение, которое назовем рекордом, сравнивается с очередным допустимым решением. Понятно, что это очень неэффективный способ решения экстремальных задач. Так как приходится сравнивать друг с другом все решения, которых может оказаться слишком много. А в случае,

когда задача непрерывна и множество допустимых решений континуально, не очень понятно как реализовать такую стратегию решения. Возникающие трудности можно попытаться обойти, если воспользоваться методом ветвей и границ (МВГ). Данный метод основан на переборе допустимых решений, в процессе которого рекорд сравнивается с подмножествами допустимых решений. Этот алгоритм осуществляет поиск оптимального решения посредством последовательного разбиения множества допустимых решений на под множества меньшей мощности. Нижние оценки на значения целевой функции на этих подмножествах сравниваются с текущим рекордным значением целевой функции. Ясно, что подмножества решений, у которых нижние оценки больше текущего рекордного значения, не могут содержать оптимального решения и должны быть отброшены. В приводимом ниже описании метода ветвей и границ предположение о конечности множества Q не используется. Более важно свойство разложимости, которое описывается ниже,

и предположение о конечности числа атомарных множеств. Атомарным множеством назовем подмножество Q, на котором исходная задача легко решается точно или приближенно. Подмножество Q допустимых решений назовем разложимым, если оно представимо в виде объединения некоторого конечного набора атомарных множеств. Обозначим через x(d) наилучшее решение задачи на атомарном множестве d, найденное с помощью некоторого алгоритма. Функцией ветвления b(d) назовем функцию, определенную на разложимых подмножествах множества Q и ставящую в соответствие множеству d определенное его разбиение на несобственные разложимые подмножества. Нижней границей назовем вещественную функцию H(d), определеннуюна разложимых подмножествах множества Q и такую, что

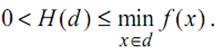, функция невозрастающая.

Схема метода.

Состоит из конечной последовательности однотипных шагов. На каждом шаге расм. Разбиение d1…. dl множества еще нерассмотренных допустимых решений и некоторый рекорд x^0. Пусть к следующему шагу есть разбиение d1…dl и рекорд x^0, проверяем элементы разбиения на наличие решения со значением лучше рекорда. Если есть новый рекорд, то обновляем рекорд и проверяем следующий случай, если все случаи проверены, то рекорд – есть решение задачи. При разработке алгоритма МВГ необходимо определить:

– атомарные множества решений;

– способ задания подмножеств решений;

– функцию ветвления;

– способ вычисления нижней границы;

– функцию выбора наилучшего решения;

– правила выбора перспективного элемента разбиения.

Не нашли, что искали? Воспользуйтесь поиском: