
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расширенное определение
Обычная формула Бернули применима на случай когда при каждом испытании возможно одно из двух cобытий. Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из 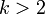 событий с вероятностью
событий с вероятностью  , где
, где  . Вероятность появления
. Вероятность появления  раз первого события и
раз первого события и  - второго и
- второго и 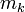 раз k-го находится по формуле
раз k-го находится по формуле
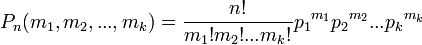 ,
,
где 
Свойства
Пусть p - вероятность успеха в схеме Бернулли, q=1-p. Тогда самым вероятным среди событий 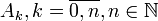 является событие
является событие  , где
, где  можно найти с неравенства
можно найти с неравенства  .
.
Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний  . При больших значениях
. При больших значениях  пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
Теорема. Если вероятность  наступления события
наступления события  в каждом испытании постоянна и мала, а число независимых испытаний
в каждом испытании постоянна и мала, а число независимых испытаний  достаточно велико, то вероятность наступления события
достаточно велико, то вероятность наступления события  ровно
ровно  раз приближенно равна
раз приближенно равна
 ,(3.4)
,(3.4)
где 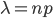 .
.
Доказательство. Пусть даны вероятность наступления события  в одном испытании
в одном испытании  и число независимых испытаний
и число независимых испытаний  . Обозначим
. Обозначим 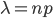 . Откуда
. Откуда  . Подставим это выражение в формулу Бернулли:
. Подставим это выражение в формулу Бернулли:

При достаточно большом!!n,, и сравнительно небольшом!!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

Учитывая то, что  достаточно велико, правую часть этого выражения можно рассмотреть при
достаточно велико, правую часть этого выражения можно рассмотреть при  , т.е. найти предел
, т.е. найти предел

Тогда получим
 (3.5)
(3.5)
Пример. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.
Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).
Находим  .
.
Воспользуемся формулой Пуассона

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
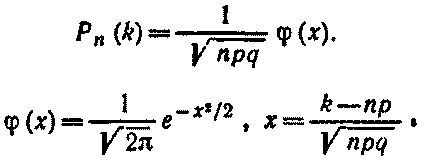
Для определения значений φ(x) можно воспользоваться специальной таблицей.
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
P(k1;k2)=Φ(x'') - Φ(x')
Здесь
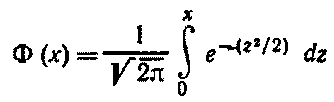
- функция Лапласа

Значения функции Лапласа находят по специальной таблице.
Пример. Найти вероятность того, что событие А насту пит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение. По условию, n=243; k = 70; р =0,25; q= 0,75. Так как n=243 - достаточно большое число, воспользуемся локальной теоремой Лапласа:

где х = (k—np)/ √npq.
Найдем значение х

По таблице п найдем ф(1,37) =0,1561. Искомая вероятность
P(243)(70) = 1/6,75*0,1561 =0,0231.
Не нашли, что искали? Воспользуйтесь поиском: