Определение нагрузок на головку балансира станка-качалки. Определение нагрузок производится по различным теориям, которые, в основном, делятся на две группы: статические и динамические

Определение нагрузок производится по различным теориям, которые, в основном, делятся на две группы: статические и динамические. Согласно исследованиям А. Н. Адонина [1] граница между статическим и динамическим режимами откачки находится в интервале (переходная зона) параметра Коши:

,

где а - скорость звука в штангах.

Для одноразмерной колонны а = 4600 м/с, для двухступенчатой а = 4900 м/с; для трехступенчатой а = 5300 м/с. В настоящее время применяют в основном режимы при μ = 0,5 При μ > 0,7 многие формулы просто неприемлемы из-за больших резонансных усилий.

Максимальная нагрузка по статической теории (формула Муравьева И. М.)

, (2.13)

где Рж - вес столба жидкости над плунжером, высотой, равной hд, с учетом буферного давления Рб,

; (2.14)

b - коэффициент облегчения штанг в жидкости,

; (2.15)

m - фактор динамичности,

, (2.16)

где S_A - длина хода точки подвеса штанг; n - число качаний в минуту.

Вес штанг в воздухе

.

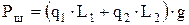Минимальная нагрузка будет, очевидно, при начале хода штанг вниз, когда вес жидкости не действует на штанги, а динамический фактор вычитается:

, (2.17)

Определение нагрузок по формулам А. С. Вирновского. Согласно исследованиям А. Н. Адонина [1] они дают наилучшее совпадение с опытными результатами замеров нагрузки:

(2.18)

где Рж - вес столба жидкости высотой hд с учетом буферного давления с площадью, равной Fпл; Р'ж = (Fпл - fшт) ·ρж·g·L - вес столба жидкости в кольцевом пространстве; Fпл, fшт - площадь поперечного сечения плунжера и штанг соответственно; L - глубина спуска насоса; Ршт - вес колонны штанг в воз­духе; Р'шт - вес колонны штанг в жидкости.

Формула для минимальной нагрузки получается из преды­дущей (2.18), если положить Р'ж = 0, Рж = 0, а кинематические коэффициенты α1 и а1 заменить на аналогичные α2 и а2 при ходе штанг вниз и переменить у двух последних членов знаки на противоположные:

(2.19)

Здесь S_А - длина хода точки подвеса штанг; Ршт - вес ко­лонны штанг в воздухе; Р'шт - вес колонны штанг в жидкости; α1, α2, а1, а2 - кинематические коэффициенты А. С. Вирнов-ского [1,23],

,

где Vmax - действительная максимальная скорость точки подвеса штанг; 1 - при ходе вверх; 2 - при ходе вниз; D, dшт - диаметры насоса и штанг; ω - угловая скорость в 1/с, ω = π·n / 30; λшт - удлинение штанг от веса столба жидкости,

; (2.19')

- коэффициент изменения сечения потока жидкости при переходе от насоса в трубы;
Fтр - площадь внутреннего канала труб; fтр - площадь сечения труб по металлу;

- коэффициент отношения площадей.

Если расчет ведется для ступенчатой колонны, то вместо fшт нужно брать

, (2.20)

где ε1, ε2, εn - доли ступенчатой колонны штанг, Σεi = 1.

Упрощенные А. Н. Адониным формулы А. С. Вирновского можно использовать для широкого диапазона S_А < 5м; n =24 мин^-1, D < 93 мм:

;

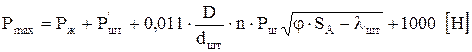. (2.21)

Не нашли, что искали? Воспользуйтесь поиском: