Расчет производительности и определение коэффициента подачи ШГНУ. Формула производительности по элементарной теории [27|

Формула производительности по элементарной теории [27|

(2.37)

где F - площадь поперечного сечения плунжера; n - число двойных ходов в мин; S_А - длина хода точки подвеса штанг; λшт, λтр - удлинение насосных штанг и труб от веса столба жидкости,

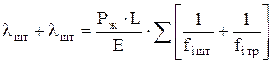, (2.38)

где Рж = hд·ρж·F·g - вес столба жидкости над плунжером; L - глубина подвески насоса; E = 2,1·10¹¹ Н/м² - модуль упругости стали.

Последний член формулы (2.37) учитывает увеличение длины хода плунжера за счет инерционных сил - δи:

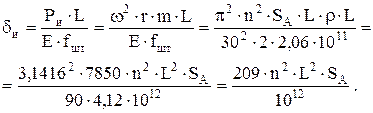
Учитывая массу муфт штанг,

Производительность по элементарной теории (А. Н. Адонина) [1]

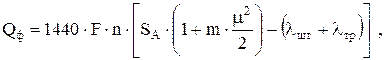(2.39)

где

- параметр Коши; а - скорость звука в колонне штанг; m - коэффициент, учитывающий влияние инерции

столба жидкости.

Для Dпл < 43 мм, m = 1,0;

Dпл = 55 мм, m = 1,5;

Dпл = 68 - 70 мм, m = 2,0;

Dпл=82 мм, m = 4,0;

Dпл = 93мм, m = 3,0;

Dпл = 120мм, m = 4,0.

Формула производительности А. С. Вирновского

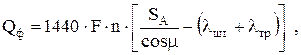(2.40)

где член S_А/cosμ, выражающий перемещение плунжера при отсутствии статических удлинений λш и λтр, получен для вынужденных колебаний «свободной» штанги, т. е. штанги без плунжера, при гармоническом законе движения балансира. Отсюда следует, что формула (2.40) применима лишь для насосов малого диаметра (D < 43 мм и μ < 0,785).

Формула (2.39) приемлема для всех диаметров плунжера при μ < 0,55. При больших значениях μ, она дает погрешность около 9% [1].

При откачке высоковязкой жидкости или при больших скоростях откачки жидкости обычной вязкости большое значение приобретают силы гидродинамического трения. Онл возникают при движении штанг в жидкости, жидкости в трубах, а также в клапанах насоса. Для этих условии соответствующую формулу получил А. С. Вирновский:

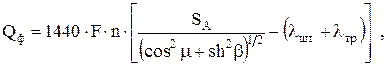(2.41)

где

; h - константа трения, с^-1 (h = 0,2 - 1,0 с^-1);

- гиперболический синус.

При (β = 0 из формулы (2.41) получается формула (2.40).

В случае наличия силы сопротивления, вызванной сопротивлением потоку жидкости в нагнетательном клапане и трением плунжера о цилиндр, в формулах (2.37) - (2.41) необходимо λтр +λшт заменить на

, (2.42)

При двухступенчатой колонне штанг с учетом сопротивления движению штанг в вязкой жидкости

(2.43)

где Sпл определяется по зависимости (2.33).

Теоретическая производительность глубинно-насосной установки определяется по формуле [19, 27]:

(2.43')

Коэффициент подачи ШГНУ

. (2.44)

Определяя Qф по формуле (2.37), получим

, (2.45)

.

Для облегчения расчетов можно пользоваться номограммой Иванова [27, с. 52]. По этой номограмме можно ориентировочно найти любой из пяти параметров работы ШГНУ (Q, D, S, n, η) при четырех известных других.

Задача 12. Определить производительность и коэффициент подачи ШГНУ по различным формулам и сравнить их.

Дано: глубина скважины Н = 1500 м;

глубина спуска насоса L = 1400 м;

диаметр насоса Dпл = 38 мм;

диаметр штанг dшт = 19 мм; dтр = 60 мм;

плотность нефти ρн = 850 кг/м³;

длина хода точки подвеса штанг S_A = 2,1 м;

число качаний n = 10 мин^-1;

забойное давление Рзаб = 30 кгс/см²;

содержание воды nв = 0,25.

Решение. Плотность жидкости

.

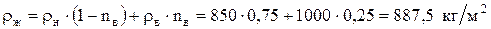Расстояние до динамического уровня

.

Вес столба жидкости над плунжером, полагая, что Рбуф = 0,

.

1. 1. Определим производительность по теории А. М. Юрчука (формула (2.37)).

Предварительно определим:

;

;

;

;

.

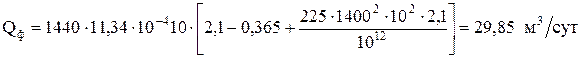2. 2. Производительность по формуле (2.39) А. Н. Адонина

.

Режим откачки статический, Dпл < 43, m = 1,

.

3. 3. Производительность по формуле (2.40) А. С. Вирновcкого

;

.

4. Определим производительность по формуле (2.41) при условии, что h = 0,6 с^-1:

;

;

.

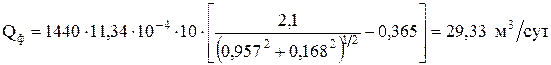5. Определим производительность с учетом формулы (2.42), полагая, что сила сопротивления движению плунжера Рc = 4 кН.

По формуле (2.29) определим λсж штанг:

.

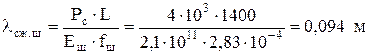Изгиб штанг под действием Рс по формуле (2.32)

,

где

;

;

.

По формуле (2.42) найдем λ:

.

Найдем производительность по формуле (2.40):

.

Таким образом, производительность по первым трем формулам не отличается. Существенные отличия наблюдаем при наличии силы сопротивления (формула (2.42)) и с учетом гидродинамического сопротивления при высоких константах трения h > 0,6 с^-1.

6. Определим коэффициент подачи:

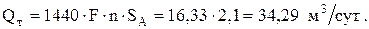
Коэффициент подачи по формуле (2.44)

c учетом вязкости жидкости

с учетом силы сопротивления

Не нашли, что искали? Воспользуйтесь поиском: