СВОЙСТВА МНОЖЕСТВ ВЫВОДИМЫХ СЛОВ

Из всех слов, выводимых в произвольной системе Поста, выделяются подмножества таких слов, которые могут считаться окончательными результатами вычислений.

В процессе вывода таких окончательных слов в системах Поста приходится использовать и другие слова, которые можно рассматривать как промежуточные или вспомогательные слова.

В простейшем случае заключительными считаются все слова, которые не содержат символов вспомогательного алфавита.

В других случаях заключительные слова должны иметь специальную структуру.

Например, рассмотрим систему Поста, в которой выводятся все такие пары двоичных последовательностей (x, y), являющихся правильными записями неотрицательных целых чисел.

В этой системе все выводимые слова, начинающиеся с буквы N, являются вспомогательными. Они представляют правильные записи целых неотрицательных чисел в двоичной системе, выводимых с помощью продукций:

p₁ = N 0; p₂ = N 1; p₃ = N 11; p₄ = N 10;

p₅ = ; p₆ = .

Пары целых неотрицательных чисел (x, y) выводятся с помощью продукции:

p₇ = .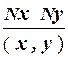

Приведенная система Поста имеет основной алфавит
A = { 0, 1, (,),, } и вспомогательный алфавит V = { N }.

Результатами в такой системе являются только такие выводимые слова, которые не содержат символа N.

Выводимые в системе вспомогательные слова имеют вид Nx.

Множество всех слов, выводимых в произвольной системе Поста с непустым вспомогательным алфавитом, разбивается на два класса: это класс слов, содержащих символы вспомогательного алфавита, и класс слов, состоящих только из символов основного алфавита.

Слова из первого класса называются нетерминальными словами системы Поста; из второго класса - терминальными, или заключительными.

В дальнейшем обозначение W_P будет применяться для множества слов в основном алфавите, которые выводятся в системе Поста P. Другие слова, выводимые в системе Поста P и содержащие вспомогательные символы рассматриваются как промежуточные в выводах, позволяющие организовать вывод заключительных слов.

Рассмотрим ещё один пример системы Поста, в которой выводятся все возможные пары слов вида (, ), где - это произвольная последовательность из нулей и единиц, а - двоичная запись числа, равного длине последовательности .

Выпишем множество продукций соответствующей системы Поста.

1. Вспомогательные продукции, позволяющие выводить правильные двоичные записи неотрицательных целых чисел:

p₁= N 1; p₂= N 0; p₃= N 11; p₄ = N 10; p₅: ; p₆: .

2. Вспомогательные продукции, позволяющие выводить слова вида S (x) = y, где x и y - это правильные двоичные записи неотрицательных целых чисел и у = x + 1:

p₇: S (0) = 1; p₈: ; p₉: .

3. Основные продукции, позволяющие выводить пары, слов (, ), которые являются заключительными:

p₁₀: (0, 1); p₁₁: (1, 1);

p₁₂: ; p₁₃: .

Здесь символы N и S образуют вспомогательный алфавит, а x, y, z - алфавит переменных. Остальные символы составляют основной алфавит.

Упражнение. Привести пример множества слов в алфавите { 0, 1 }, которое выводится только в таких системах Поста, которые имеют непустой вспомогательный алфавит.

Рассмотрим класс всех таких множеств слов, каждое из которых выводится в некоторой системе Поста. Покажем, что этот класс замкнут относительно операций объединения и пересечения множеств.

Справедливость приведенного свойства вытекает из теоремы 9.2.

ТЕОРЕМА 9.2

Если W ₁ и W ₂- множества слов, выводимых в системах P ₁ и P ₂ соответственно, то найдутся такие системы P_U и P_I, в которых выводятся соответственно множества

W ₁ È W ₂ и W ₁Ç W ₂.

Доказательство

Пусть R и Q - символы, которые не встречаются среди символов алфавитов систем P ₁ и P ₂.

1. Определим систему P_U. Основной алфавит и алфавит переменных этой системы получаются объединениями основных алфавитов и алфавитов переменных систем P ₁ и P ₂.

Вспомогательный алфавит системы P_U состоит из символов вспомогательных алфавитов для P ₁ и P ₂, а также символов R и Q.

Множество продукций системы P_U состоит из продукций, получаемых из продукций P ₁ приписыванием всем образцам слева символа R, а также продукций, получаемых из продукций системы P ₂ с помощью аналогичного приписывания символа Q.

Кроме того, в P_U добавлены продукции:

и .

Покажем, что в системе P_U выводятся те и только те слова, которые принадлежат W ₁ 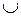W _2.

Это следует из того, что некоторое слово x выводится в системе P_U тогда и только тогда, когда в этой системе выводится либо слово Rx, либо слово Qx.

Последнее равносильно тому, что x выводится либо в P ₁, либо в P ₂. Поэтому в P_U выводится множество слов W ₁ W ₂.

2. Определим систему Поста P_I.

Алфавиты этой системы определяются так же, как это было определено для системы P_U.

Продукции системы P_I получаются из продукций P ₁ и P ₂ приписыванием ко всем образцам в них слева символов R и Q соответственно.

К этим продукциям добавляется еще одна

.

Видно, что в системе P_I выводятся такие и только такие слова x, которые могут быть выведены как в P _1, так и в P ₂.

Поэтому множество слов, выводимых в системе P_I, равно
W ₁ W ₂.

Не нашли, что искали? Воспользуйтесь поиском: