Доказательство окончено. Вспомогательные символы R и Q использованы для того, чтобы продукция, получаемая из продукции одной из систем описанным в доказательстве преобразованием

Вспомогательные символы R и Q использованы для того, чтобы продукция, получаемая из продукции одной из систем описанным в доказательстве преобразованием, могла применяться только к таким совокупностям слов, которые выводятся с помощью преобразованных продукций той же системы.

Если, например, при построении системы P_U в качестве множества продукций для P_U взять объединение множеств неизмененных продукций систем P ₁ и P ₂, то можно получить систему, в которой выводятся слова, не входящие в W ₁ 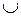W ₂.

В качестве примера рассмотрим системы P ₁ и P ₂ со следующими совокупностями продукций:

p_1,1: 1, p_1,2: ; (1)

p_2,1: 0, p_2,2: . (2)

Тогда с помощью продукций (1) системы P ₁ можно выводить слова, составленные только из единиц, а при помощи множества (2) системы P ₂ - слова, которые имеют конечное число нулей.

Однако продукции p_1,1, p_{1, 2}, p_2,1, p_2,2, используемые совместно, позволяют выводить любые слова, состоящие из нулей и единиц.

Семейство классов слов, выводимых в системах Поста, не замкнуто относительно операции взятия дополнений таких множеств.

Это означает, что существует такая система P = (A, B, V, P), для которой множество A * \ W_P не выводится ни в одной системе Поста. Доказательство этого факта будем приведено ниже после изучения связи множеств слов, выводимых в системах Поста и множества частично-рекурсивных функций.

Всякое множества W - таких слов в некотором основном алфавите A, что W и его дополнение до A * выводимы в некоторых системах Поста, является разрешимым.

Справедливость последнего свойства вытекает из следующей теоремы.

ТЕОРЕМА 9.3

Пусть W - такое множество слов в основном алфавите A, что множества слов W и A* \ W выводятся в системах Поста P ₁ и P ₂.

Тогда существует алгоритм, который по любому слову A* за конечное число шагов работы определяет принадлежность множеству W.

Доказательство

Приведем описание процедуры, позволяющей распознавать слова, содержащиеся во множестве W.

Воспользуемся двумя экземплярами алгоритма построения всех конечных выводов в произвольных системах Поста.

С помощью первого из этих алгоритмов будем строить все такие выводы в системе P ₁, а с помощью второго - все выводы в системе P ₂.

Такие два параллельно работающих алгоритма позволяют последовательно выводить все слова из множеств W и A* \ W.

Поскольку произвольное A* содержится либо во множестве W, либо в дополнении этого множества, то содержится либо в выводах системы P _1, либо в выводах системы P ₂.

В первом случае Î W. Во втором случае Î A* \ W.

Поэтому для любого Î A* за конечное число шагов работы приведенного алгоритма устанавливается принадлежность множеству W. Значит, множество W является разрешимым.

Не нашли, что искали? Воспользуйтесь поиском: