
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Доказательство окончено.
Ранее уже отмечалось, что множество классов слов, выводимых в системах Поста, не является замкнутым относительно операции взятия дополнения до множества всех слов в заданном основном алфавите. Такое свойство множеств выводимых слов связано существованием неразрешимых множеств слов, выводимых в системах Поста.
ФУНКЦИИ, ВЫЧИСЛЯЕМЫЕ СИСТЕМАМИ ПОСТА
Пусть P = (A, B, V, P) - система Поста, основной алфавит, который вместе с другими символами содержит символы f,), (и символ запятой -,. Здесь f - функциональный символ, обозначающий некоторую функцию.
ОПРЕДЕЛЕНИЕ
Словарная функция f: (A*) n ® A* вычисляется системой P, если: "  1,...,
1,...,  n Î A* (f (
n Î A* (f ( 1,...,
1,...,  n) =
n) =  n+ 1
n+ 1  в системе P выводится слово ″ f (
в системе P выводится слово ″ f ( 1,...,
1,...,  n) =
n) =  n+ 1″),
n+ 1″),
То есть функция f, вычисляемая системой Поста P, отображает набор ( 1,...,
1,...,  n), составленный из - слов в алфавите A, в слово
n), составленный из - слов в алфавите A, в слово  n+ 1 в том же алфавите тогда и только тогда, когда в P выводима запись: ″ f (
n+ 1 в том же алфавите тогда и только тогда, когда в P выводима запись: ″ f ( 1,...,
1,...,  n) =
n) =  n+ 1″.
n+ 1″.
Иначе говоря, в системе P выводятся записи таких слов, которые представляют график отображения f.
Аналогично определяется понятие числовой функции, вычисляемой в некоторой системе Поста P.
Пусть  обозначает двоичную запись числа m.
обозначает двоичную запись числа m.
ОПРЕДЕЛЕНИЕ
Числовая функция f: Nk ® N вычисляется системой P, если " m 1,..., mk Î N (f (m 1,..., mk) = mk+ 1  в системе P выводится слово “ f (
в системе P выводится слово “ f ( 1,...,
1,...,  k) =
k) =  k+ 1“).
k+ 1“).
В качестве примера рассмотрим систему Поста, в которой вычисляется функция следования S (x) = x + 1.
Такая система имеет вид: P = (A, B, V, P), где
A = { 0, 1, S, (,), =}, B = { N }, V = { x, y }, а P - это следующие продукции.
1. Вспомогательные продукции, позволяющие выводить только правильные записи чисел из N в двоичной системе:
p1: N 0, p2: N 1, p3: N 10, p4: N 11,
p5:  , p6:
, p6:  .
.
2. Продукция, задающая правило прибавления единицы к четным числам:
p7: 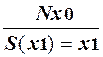 ;
;
3. Продукция, задающая правило прибавления единицы к нечётным числам (запись которых заканчивается единицей):
p8:  .
.
В частности, следующая последовательность образует вывод слова S (101) = 110:
1. N 1 аксиома p2;
2. N 10 из N 1 с помощью p5;
3. N 101 из N 10 с помощью p6;
4. S (10) = 11 из N 10 с помощью p7;
5. S (101) = 110 из N 10 и S (10) = 11 с помощью p8.
В приведенной системе вычисляется достаточно простая арифметическая функция. Однако добавление к ней небольших количеств новых продукций, использующих другие функциональные символы, позволяет получать системы Поста, вычисляющие новые, в том числе более сложные, числовые функции.
Например, для вычисления функции p (x, y) = x + y достаточно добавить к уже имеющимся продукциям следующие новые продукции:
p9:  ; p10:
; p10:  .
.
В продукции p9 представлено правило прибавления к произвольному числу минимального неотрицательного целого числа.
В  10 записано рекурсивное правило сложения двух произвольных чисел, использующего значение суммы первого числа и числа на единицу меньше, чем второе слагаемое.
10 записано рекурсивное правило сложения двух произвольных чисел, использующего значение суммы первого числа и числа на единицу меньше, чем второе слагаемое.
Продукции p9 и p10 соответствуют рекурсивному определению функции p (x, y). Из них продукция p9 задаёт граничное условие, а p10 представляет рекурсивное правило, в котором значение p (x, y) выражается через значение p (x, v), где v = y - 1.
Используя продукции, позволяющие вычислять функции S и p, можно определять системы Поста, в которых вычисляются и другие функции.
Например, функция усеченной разности: d (x, y) = x -y вычисляется с помощью двух продукций, добавляемых к продукциям p1 - p10:
p11: 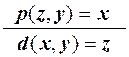 , p12:
, p12:  .
.
Множество всех числовых функций, вычисляемых системами Поста, совпадает с классом частично-рекурсивных функций.
Справедливость приведенного утверждения следует из теоремы 9.4.
ТЕОРЕМА 9.4
Всякая частично-рекурсивная функция вычислима в некоторой системе Поста.
Доказательство
Проведем доказательство сформулированной теоремы по этапам определения частично-рекурсивных функций.
1. Покажем, что все примитивные функции вычисляются системами Поста.
Действительно, функция O (x) вычисляется с помощью продукции p: 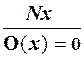 , добавленной к рассмотренным ранее продукциям p1 - p6, позволяющим выводить все правильные двоичные записи натуральных чисел.
, добавленной к рассмотренным ранее продукциям p1 - p6, позволяющим выводить все правильные двоичные записи натуральных чисел.
Функция S (x) вычисляется с помощью продукций p1 - p8, а 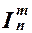 (x 1,..., xn) вычисляется с помощью дополнительной продукции
(x 1,..., xn) вычисляется с помощью дополнительной продукции
 .
.
2. Покажем, что всякая суперпозиция функций, вычислимых системами Поста, вычисляется в некоторой системе Поста.
Пусть заданы функции
f (x 1,..., xn), j1(x 1,1,..., x 1, m 1),..., j n (xn ,1,..., xn , m n), которые вычисляются системами Поста P 0, P 1,..., P n соответственно.
Покажем, что функция h (xi 1,..., xi k) =
= f (j1(x 1,1,..., x 1, m 1),..., j n (xn ,1,..., xn , m n)),
где xi 1,..., xi k - все различные переменные функций j1,..., j n, также вычислима некоторой системой Поста.
Обозначим как G 0, G 1,..., G n - вспомогательные символы, которые не встречаются среди символов алфавитов систем Поста P 0, P 1,..., P n.
Модифицируем продукции этих систем Поста, приписав всем образцам каждой продукции из P iслева символ G i.
Рассмотрим систему Поста P, продукциями которой являются все модифицированные продукции систем P 0, P 1,..., P n, а также продукция
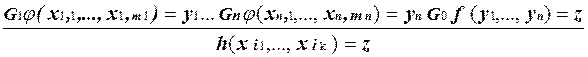 .
.
Очевидно, что P вычисляет функцию h.
3. Покажем, что всякая функция, выражаемая через функции, вычислимые системами Поста с помощью операции примитивной рекурсии, вычисляется некоторой системой Поста.
Пусть функция f выражается через функции g и h с помощью операции примитивной рекурсии
f (x 1,..., x n, 0) = g (x 1,..., x n)
f (x 1,..., x n, y + 1) = h (x 1,..., x n, f (x 1,..., x n, y)).
Пусть функции g и h вычисляются системами Поста Pg и Ph.
Возьмем два вспомогательных символа Gg и Gh, не встречающиеся среди символов алфавитов систем Pg и Ph.
Модифицируем продукции систем Pg и Ph, приписывая всем образцам в них слева соответственно символы Gg и Gh.
Рассмотрим систему Поста P f, в которую включим модифицированные продукции систем Pg и Ph, продукции системы, вычисляющей функцию S (x) = x + 1, помеченные еще одним вспомогательным символом Gs. Для этого символа также предполагаем, что он не встречается среди символов всех рассматриваемых систем Поста.
Добавим к этим продукциям еще две
 ; (1)
; (1)
 (2).
(2).
Нетрудно видеть, что такие продукции соответствуют соотношениям схемы примитивной рекурсии, а P f вычисляет функцию f.
4. Покажем, что если функция f выражается через функцию, вычислимую некоторой системой Поста, с помощью операции минимизации, то она также вычисляется некоторой системой Поста.
Пусть f (x 1,..., xn+ 1) = m t (g (x 1,..., xn, t) = xn +1) и функция g (x 1,..., xn+ 1) вычисляется продукционной системой Pg. Построим систему Поста P f, которая вычисляет
f (x 1,..., xn+ 1).
Включим в Pf продукции систем, вычисляющих функции S (x) и g (x 1,..., x n + 1), а также добавим к ним продукции такой системы Поста, в которой выводятся пары неравных целых неотрицательных чисел: x <> y. Построение такой системы предлагалось ранее в упражнении.
Модифицируем такие продукции так, чтобы никакие слова, выводимые в одной системе, не могли использоваться в качестве посылок продукций других систем. Например, это можно сделать, приписывая образцам продукций разных систем разные вспомогательные символы.
Добавим к указанным продукциям новые продукции:
 (1)
(1)
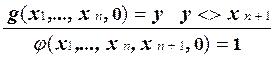 (2)
(2)
 ; (3)
; (3)
 .(4)
.(4)
Эти продукции позволяют вычислять вспомогательную функцию  , которая принимает значение 0 только для такого наименьшего значения t, при котором
, которая принимает значение 0 только для такого наименьшего значения t, при котором
g (x 1,..., x n, t) = xn+ 1 и все значения g (x 1,..., xn, i) для i < t являются определенными.
Для вычисления значений функции f используются следующие две продукции:
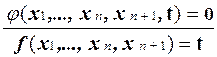 ; (5)
; (5)
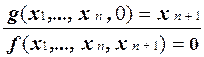 . (6)
. (6)
Построенная система Поста вычисляет функцию f.
По определению, всякая частично-рекурсивная функция может быть выражена через простейшие функции с помощью конечного числа применений операций суперпозиции, примитивной рекурсии и минимизации.
Поскольку все простейшие функции вычислимы системами Поста и применение перечисленных операций к функциям, вычислимым системами Поста, приводит к функциям, вычислимым такими системами, то теорема доказана.
Не нашли, что искали? Воспользуйтесь поиском: