
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теор.(необход.усл.экстремума).
Билет 1.
Комплексные числа.
Комлексным числом Z наз. число z=x+iy, где x, y  R.
R.
Мн-во  комплексных чисел – С, R
комплексных чисел – С, R  C, x–действ. часть, y – мнимая часть.
C, x–действ. часть, y – мнимая часть.
Расстояние от z(x,y) до начала корд. наз. модулем комп. числа Z.  Аргументом числа Z
Аргументом числа Z  0, наз угол
0, наз угол  , кот-й образует радиус-вектор точки Z и полож направл оси OX.
, кот-й образует радиус-вектор точки Z и полож направл оси OX.
Argz = argz (главное знач аргумента) + 2  k k
k k  Z
Z
-  <argz<
<argz< 
argz = 
z = x+iy=zcos  +izin
+izin  =z(cos
=z(cos  +isin
+isin  )
)
z=r(cos  + isin
+ isin  ) (!)
) (!)
z1 = r1(cos  + isin
+ isin  )
)
z2 = r2(cos  + isin
+ isin  ) тогда
) тогда
z1*z2 = r1*r2(cos( 1+
1+  2) + isin(
2) + isin( 1+
1+  2)
2)
zn = rn(cos(n  ) + isin(n
) + isin(n  )
)

 - Формула Муавра (!)
- Формула Муавра (!)


Формулы Эйлера:
 ;
;  (!)
(!)
 ;
;  ;
;  ;
;

Билет 20.
Предел функции нескольких переменных.
Опр. т. А наз. пределом посл-ти (Mn) если  для любого Е(эпсилон) сущ. N-N(E); любое n>=N(E) => p(Mn,A) < E;
для любого Е(эпсилон) сущ. N-N(E); любое n>=N(E) => p(Mn,A) < E;  ;
;  (число)
(число)
(x1, x2, …,xm)-независимые переменные.
Опр по Коши: число b наз пределом ф-ии u=f(M) в т. А (при  ), если для любого Е > 0 сущ.
), если для любого Е > 0 сущ.  , для любого
, для любого 
Опр по Гейне: число b наз пределом посл-ти ф-ии u=f(M) в т. А, если для любого (Mn), 
 A(a1, a2,…, am)
A(a1, a2,…, am)
Теор. Если сущ.  и сущ.
и сущ.  , то сущ.
, то сущ.  , причем
, причем 
Опр. u=f(M) наз. непрерывной в т. А, если 
M(x1, x2, …,xn)  ;
;  …
…  ; A(a1, a2, …,an)
; A(a1, a2, …,an)

Опр2. u=f(M) наз. непрерывной в т. А, если 
Точка в к-й ф-я не определена или не является непрерывной, наз. точками разрыва этой ф-ии.
(24) Геометр. смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.


f(x,y)=f(x0,y0)+A∆x+B∆x+o(ρ); z0=f(x0,y0); z=f(x,y); ∆x=x-x0, ∆y=y-y0;
z0=z0+A(x-x0)+B(y-y0); z0-z=A(x-x0)+B(y-y0);
z0-z=fx‘(x0,y0)(x-x0)+fy‘(x0,y0)(y-y0)-ур-ние касательн. плоскости в поверхности.
z=f(x,y) (x0,y0,z0).
Нормалью к поверхн. в данной точке М0(x0,y0,z0) назыв. прямая, проходящая через эту точку перпенд. к касат.
(x-x0)/fx‘(x0,y0)=(y-y0)/fy‘(x0,y0)=(z-z0)/(-1) – ур-ние нормали
(x-x0)/fx‘(x0,y0,z0)=(y-y0)/fy‘(x0,y0,z0)=(z-z0)/fz‘(x0,y0,z0)
Билет 2.
Многочлены.
Многочлен (полином) относительно переменной z - это 
2z4-5z3+2z=(z2-1)(2 z2-5z+2)+(-3z-2)
Qm(z) Tk(z) Rc(z)
Значит Pn(z) = Qm(z) Tk(z) + Rc(z) (*), где m<=n m+k=n, l<n;
Если Rc(z) = 0, то Pn(z) делится на Qm(z).
Назовем компл. число z1 корнем многочл. Pn(z), если Pn(z1).
Теор. БЕЗУ: многочлен не нулевой степени Pn(z) делится на двучлен z-z1, тогда и только тогда, когда z1 является корнем Pn(z).
Запишем (*) для Pn(z) и z-z1: Pn(z) = (z-z1)Tn-1(z)+ Rc(z) => z:=z1.
Основная теорема алгебры(Гаусса): всякий многочлен Pn(z) не нулевой степени имеет по крайней мере 1 комплексный корень.
Компл. число z1 наз. корнем кратности к1 многочл. Pn(z), если
Pn(z) = (z-z1)к1Тn-k1(z)
Следствие: Многочл. Pn(z) имеет n комлексных корней с учетом их кратности:
Pn(z) = an(z-z1)к1(z-z2)к2…
Пусть z1 – корень Pn(z) с действ. коэф-ми, тогда  корень Pn(z)
корень Pn(z)
Pn( )=
)=  =
=  =0
=0
Комплексно-сопряж. корни входят в разложение многочлена парами.
(z-z1)(z-  )=z2+p1z+q1
)=z2+p1z+q1
Pn(x) – с действ. коэф.
Pn(x)=an(x-x1)k1(x-x2)k2*…*(x-xl)kl(x2+p1x+q1)R1(x2+p2x+q2)R2*…*(x2+pmx+qm)Rm
x1, x2,…,xn – действ. корни
k1, k2,…,kn – их кратности
P1, P2,…,Pn, q1, q2,…,qn – действ. числа
k1+k2+…+kl+2R1+2R2+…+2Rm = n
Билет 33.
Замена переменной в двойном интеграле.

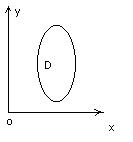
 (*)
(*)
Свойства
1) x(u,v), y(u,v) – взаимно однозначны
2) x(u,v), y(u,v) – непрерывные, непр. частн. пр-е 1-го порядка
3) 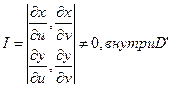


P1: x(u,v), y(u,v)
P2: x(u+∆u,v), y(u+∆u,v)





I – Якобиан(Якоби)
Модуль I – коэффициет растяжения площади в т. с координатами u и v при отображении D на D’.

Вычисление в полярной сист координат.
 ,
, 



a) 
 b)
b) 
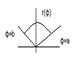
c) 
Билет 38.
Формула Грина.
Область наз. односвязной если в ней любой замкнутый контур может быть стянут в точку с помощью непрерывной деформации, при к-й не границы области не пересекаютя.
Область D наз. односвяз., если каков бы ни был замкн. контур l, лежащий внутри этой области, ограниченная этим контуром конечн. часть пл-ти целиком принадл. D.
Порстая область: замкн. пл-ть D (обл. вместе с её границами) – её можно разбить на конечное число как y- так и x- трапецивидных областей.
Например: круг, прямоугольник, кольцо.
Теор. Грина: пусть P(x,y), Q(x,y) и  и
и  непрерывны в простой области D тогда
непрерывны в простой области D тогда

где L – граница области D, к-я обходится в положительном направлении.
Док-во
Предположим D – односвяз. область, огр. L – полож. ориентир. Предположим, что оюл. D такова, что прямые параллельн. осям пересекают ее не более, чем в 2-х точках.

Для I2 – аналогично.
Формула Грина имеет место для любой простой области.
Если контур обходится в обратном направлении, то перед двойным интегралом ставится «-».
3) Рациональные дроби.
Опр.  , где Pn(z), Qm(z) – многочлены, наз. рациональной дробью.
, где Pn(z), Qm(z) – многочлены, наз. рациональной дробью.
n>=m – дробь неправильная; n<m – правильная.
Разложение правильной рац. дроби с комплексными коэф. на сумму простейших дробей.
Если  - правильная дробь, то
- правильная дробь, то  , где
, где
z1, z2,…, zl – разл. компл. корни
k1, k2,…, kl – их кратности
то сущ. Такие компл. числа Aik, где i=1,2,…,l; k=1,2,…,ki, то тогда

Разложение простой рац. дроби с действ. коэф. на сумму простейших дробей с действ. коэф.
Пусть  - правильная дробь,
- правильная дробь, 
x1, x2,…, xl – разл. компл. корни
k1, k2,…, kl – их кратности
pi2-4qi<0 для i=1…s
R1, R2,…,Rs – кратности пар корней, тогда

+Метод неопределенных коэффициентов + Метод частных значений
Билет 8.
Интегрирование тригонометрических функций.

tg(x/2)=t – универсальная тригоном. подстановка.
 ;
;  ;
;  ;
; 

Специальная тригоном. подстановка:
1) R(-sinx,cosx)dx = -R(sinx,cosx), тогда cosx = t;
2) R(sinx,-cosx)dx = -R(sinx,cosx), тогда sinx = t;
3) R(-sinx,-cosx)dx = -R(sinx,cosx), тогда tgx = t;
Интегралы вида:





I. m,n  Z, m,n >= 0;
Z, m,n >= 0;
1) Одно из чисел m, n – нечетное, тогда sinx=t,cosx=t;
2) Оба нечетные или четные - 
II. m,n  Q
Q

это дифференц. Бином
 - для гиперболических функций аналогично
- для гиперболических функций аналогично
Универсальная подстановка – th(x/2) = t, и так далее…
Билет 9.
Интегрирование иррациональных функций.
 ;
;  ; n1,n2…
; n1,n2…  N, m1,m2…
N, m1,m2…  Z
Z
 , где s-общий знаменатель дробей m1/n1, m2/n2 …
, где s-общий знаменатель дробей m1/n1, m2/n2 …
 , тогда
, тогда 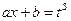



| Вид интеграла | Тригоном. подстановка | Иррацион. подстановка |

| 
| 
|

| 
| 
|

| 
| 
|

m,n,p  Q; a,b
Q; a,b  R
R
1) p  Z, тогда
Z, тогда  , где s-общий знаменатель дроби
, где s-общий знаменатель дроби
2) 
3)  , где s- знаменатель дроби
, где s- знаменатель дроби 
Во всех остальных случаях интеграл не выражается, т. е. является не берущимся.
Билет 15.
Вычисление площадей плоских фигур.
1)  В декартовой системе координат
В декартовой системе координат

 f(x)-непрерывна
f(x)-непрерывна
x=a,x=b; отр [a,b] оси оХ






2)  В параметрическом виде.
В параметрическом виде.





 ;
;  ;
; 
разбиваем:  ;
; 


3) В полярной системе координат
 ;
;  ;
;  ;
;  ;
; 
 ;
;  ;
; 

Билет 18.
Определение НИ-1.
Пусть f(x) определена на  и инт на
и инт на 
 ;
;  , т.е.
, т.е. 
Пусть 
Если этот lim существует и конечен, то говорят, что НИ-1 сходится. Если не существует или бесконечен, то расходится.
 ;
; 
Свойтсва НИ-1.
1) Аддитивность
Если  сходится, то
сходится, то  ,
,  ;
; 
2) Линейность
Если  сходится и
сходится и  сходится, то
сходится, то  сходится и
сходится и

Вычисление и преобразование НИ-1.
Формула Нбютона-Лейбница.
Если f(x) непрерывна на  и F – какая-то первообразная для ф-ции f(x), то
и F – какая-то первообразная для ф-ции f(x), то

Интегрирование по частям.
Если U,V – непрер. Диф-мы ф-ции на  , то
, то 
Исследование на сходимость.
Т1: Пусть ф-ции f(x) и g(x)  , тогда если
, тогда если  и
и  , то
, то


сходится  сходится
сходится
расходится  пасходится
пасходится
Предельный признак сравнения для НИ-1.
Т2: Пусть  ,
, 
 ;
;  , тогда если
, тогда если  конечный
конечный  , то
, то  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
При k=1  при
при 
Т3: Если  и
и  сходится, то
сходится, то  сходится.
сходится.
Определение:  называется абсолютно сходящимся, если сходится
называется абсолютно сходящимся, если сходится  .
.
Если  расходится, а
расходится, а  сходится, от
сходится, от  - неабсолютно (условно) сходящийся.
- неабсолютно (условно) сходящийся.
Главное значении.

Главным значением  называется
называется  ; VP-Value principul
; VP-Value principul

Если  и сходится, то
и сходится, то  и
и 
Билет 19.
Определение НИ-2.
f(x) определена на [a,b);  ;
;  , т.е.
, т.е. 
 называется НИ-2 и обозначается
называется НИ-2 и обозначается 
Если этот Lim существует и конечен, то говорят, что  сходится. Если он не сущ-т или бесконечен, то НИ-2 расходится.
сходится. Если он не сущ-т или бесконечен, то НИ-2 расходится.
Свойства НИ-2.
{Аналогично НИ-1. }
1) Аддитивность
Если  сходится, то
сходится, то  ,
,  ;
; 
2) Линейность
Если  сходится и
сходится и  сходится, то
сходится, то  сходится и
сходится и

Вычисление и преобразование НИ-2.
Формула Ньютона-Лейбница.
f(x) – непрерывна на [a.b); F(X) - некоторая первообразная.




Интегрирование по частям.
Если U(x) и V(x) непр. И диф-мы на [a,b), то 
Исследование на сходимость.
{Аналогично НИ-1.}
Главное значении НИ-2.
f(x) определено на 

Определение: 
Билет 22.
Дифференцируемость ф-ций нескольких переменных.
Дифференциал.
 ;
;  ;
; 
 ;
; 
Ф-ция  называется диф-м в точке
называется диф-м в точке  если ее полное приращение
если ее полное приращение  может быть представлено в виде
может быть представлено в виде  , где
, где  , А,В – числа.
, А,В – числа.
Теорема: Если  диф в точке
диф в точке  , то
, то  непрерывна в этой точке.
непрерывна в этой точке.
Док-во:  -диф-ма в т.
-диф-ма в т. 
 ;
; 
 - непрерывна в точке
- непрерывна в точке 
Теорема (необходимое условие диф): Если  диф в точке
диф в точке  , то
, то 

Док-во:  ;
;  ;
;



Теорема (достаточное условие диф): Если  имеет частные производные в некоторой окрестности т.
имеет частные производные в некоторой окрестности т.  , непрерывна в самой точке
, непрерывна в самой точке  , то она диф. В точке
, то она диф. В точке  .
.
Если  дифф. В т.
дифф. В т.  , то главная линейная, относительно приращения аргумента, часть его полного приращения называется полным диффиринциалом ф-ции
, то главная линейная, относительно приращения аргумента, часть его полного приращения называется полным диффиринциалом ф-ции  в т.
в т. 
 ;
; 
 ;
;  ;
; 
Билет 23.
Диффиренцирование сложной ф-ции нескольких переменных.
 ;
;  ;
; 
Теорема: Если ф-ция  дифф. В т.
дифф. В т. 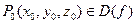 , а
, а 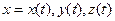 - дифф. в т.
- дифф. в т.  , то тогда
, то тогда  будет дифф. в т.
будет дифф. в т.  и
и 
Док-во:  ;
;  ;
; 
 - дифф. в т.
- дифф. в т. 
 - непрерывны в т.
- непрерывны в т.  , т.е.
, т.е.  ;
; 
 дифф. в т.
дифф. в т. 


 ;
;

 ;
;  ;
;  ;
;
 ;
; 
 ;
;

 - свойство инвариантности формы первого дифф.
- свойство инвариантности формы первого дифф.
Билет 39.
Условие независимости КРИ-2 от пути. Интегрирование полных дифференциалов.
Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны:
1)  , где L – любой замкнутый контур Д.
, где L – любой замкнутый контур Д.
2)  не зависит от пути AB.
не зависит от пути AB.
3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \
4) dP/dy=dQ/dx в области Д.
Доказательство:


где  .
.
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.

Нахождение ф-ции по ее полному дифференциалу.
Первый способ:
U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy

Второй способ:  ;
; 

{  ;
;  };
}; 
 не зависит от пути.
не зависит от пути.
Билет 40.
Физический смысл ПОВИ-2 – поток жидкости через пов-ть в единицу времени.
M (x,y,z) – вектор скорости жидкости. a (M) = P(x,y,z) i + Q (x,y,z) j + R(x,y,z) k
1)  ;
;  2)
2) 
3)  ; 4)
; 4) 
5) 
ПОВИ-2 есть поток жидкости (поток векторного поля a(M)) через ориентированную поверхность  .
.
Скалярная форма ПОВИ-2.  ;
;  ПОВИ-1 для
ПОВИ-1 для  ;
;
ПОВИ-2 для P(x,y,z), Q(x,y,z), R(x,y,z) x,y,z-пректируемое
E, F(x,y,z)=0; x=x(y,z); y=y(x,z): z=z(x,y)



Замечания: если прямая, параллельная к-л из координатных осей пересекает поверхность  более чем в одной точке, то пов-ть
более чем в одной точке, то пов-ть  следует разбить на несколько пов-тей и воспользоваться свойством аддитивности ПОВИ-2.
следует разбить на несколько пов-тей и воспользоваться свойством аддитивности ПОВИ-2.
 - ПОВИ-2
- ПОВИ-2
Формула Астроградского. Пусть V-ограниченая область, граница которой состоит из конечного числа кусочно-гладких поверхностей. Пусть ф-ции P,Q,R и их частные производные dP/dx; dQ/dy; dR/dz непрерывны в замкнутой области V, тогда справедливо следуещее равенство: 
ПОВИ-2 берется по внешней стороне пов-ти  , ограниченной областью V.
, ограниченной областью V.
Если пов-ть не замкнутая, но ее можно замкнуть простыми пов-ми, то дополнить, применить формулу Астроградского к замкнутой пов-ти, вычислить ПОВИ-2 по простым дополняющим пов-м и из интеграла по замкнутой пов-ти вычесть результат для дополнительных пов-тей.
Билет 41.
Формула Стокса.
Пусть гладкая xyz-проетируемая ориентированная поверхность  ограничена кусочно гладким контуром
ограничена кусочно гладким контуром  и пусть в некоторой 3х мерной области, содержащей в себе поверхность
и пусть в некоторой 3х мерной области, содержащей в себе поверхность  , ф-ции P,Q,R и их частные проихводные непрерывны, тогда справедливо следующее:
, ф-ции P,Q,R и их частные проихводные непрерывны, тогда справедливо следующее:  ,
,
где направление обхода контура  осуществляется в положительном направлении.
осуществляется в положительном направлении.
Если граница  состоит из нескольких контуров, то формула Стокса остается в силе. При этом в левой части надо написать сумму интегралов по всем контурам, пробегаемым в положительном направлении.
состоит из нескольких контуров, то формула Стокса остается в силе. При этом в левой части надо написать сумму интегралов по всем контурам, пробегаемым в положительном направлении.
Для вычисления интегралов по замкнутому контуру  можно выбрать любую поверхность
можно выбрать любую поверхность  , ограниченную контуром
, ограниченную контуром  . Разумно выбирать поверхность простого вида.
. Разумно выбирать поверхность простого вида.
Условие независимости КРИ-2 от пути интегрирования.
3х мерная область V называется поверхностно односвязной, если для любого замкнутого контура  , лежащего в V внутри V найдется поверхность, ограниченная
, лежащего в V внутри V найдется поверхность, ограниченная  .
.
 и их частные производные 1го порядка непрерывны в некоторой замкнутой ограниченной поверхностью односвязной области V, то след. 4 условия эквивалентны:
и их частные производные 1го порядка непрерывны в некоторой замкнутой ограниченной поверхностью односвязной области V, то след. 4 условия эквивалентны:
1)  любого замкнутого кусочногладкого контура
любого замкнутого кусочногладкого контура  -
- 
2)  не зависит от пути соединения точек А и В.
не зависит от пути соединения точек А и В.
3)  полный диф-л, где
полный диф-л, где 
4) 
Билет 28.
Условный экстремум ф-ции нескольких переменных.
Найти экстремум z, при ксловии, что x и y связаны следующим образом.
 ; x+y-1=0;
; x+y-1=0;
 (*)
(*)
 ;
;  ;
;  ;
; 
Метод множителя Ла-Гранджа.
(*) эквивалентна задаче:  , где
, где
 -множитель Ла-Гранджа;
-множитель Ла-Гранджа;  - функция Ла-Гранджа.
- функция Ла-Гранджа.

Надо исследовать  ф-ции Ла-Гранджа с учетом условия связи в диффиринциалах.
ф-ции Ла-Гранджа с учетом условия связи в диффиринциалах.
Наибольшее и наименьшее значение ф-ции в замкнутой области.
Если ф-я определена в замкнутой ограниченной области Д, то она достигает своего min и max значения, либо в стационарных точках внутри области, либо на ее границе.
Билет 29.
Интегралы по фигуре от скалярной ф-ции.
Множество называется связанным, если любые 2 из них можно соединить линией, все точки которой принадлежат данному множеству.
Под геометрической фигурой  понимается одно из следующих связных (включая границу) множеств точек (см. таблицу).
понимается одно из следующих связных (включая границу) множеств точек (см. таблицу).
Диаметром d фигуры Ф называется максимальное расстояние между двумя ее точками.
Под мерой  фигуры Ф понимается следующее (см. таблицу).
фигуры Ф понимается следующее (см. таблицу).
 Если он существует, конечен и не зависит от способа построения интегральной суммы
Если он существует, конечен и не зависит от способа построения интегральной суммы  , то он называется интегралом по фигуре Ф от скалярной ф-ции Ф(Р) и обозначается
, то он называется интегралом по фигуре Ф от скалярной ф-ции Ф(Р) и обозначается 
Теорема: Если на связной, ограниченной и содержащей граничные точки фигуре Ф скалярная ф-ция f(P) непрерывна, то интеграл по фигуре Ф существует.
Билет 30.
Свойства интегралов по фигуре от скалярной ф-ции.
1). 
2). 
3). 
4). 
 ;
;  - длина линии L;
- длина линии L;  ;
;  ;
; 
5). Если  то
то 
6). Если  , то
, то 
7). Если  , то
, то 
8). Теорема о среднем: Если f(p) непрерывна на фигуре Ф, причем Ф – ограничена о содержит граничные точки, то 
Геометрические и физические прилажения интегралов по фигуое от скалярной ф-ции.
 - материальная фигура
- материальная фигура
 - плотность материальной йигуры Ф
- плотность материальной йигуры Ф






Билет 31.
Криволинейный интеграл 1го рода.
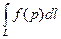 1).
1).  ;
;  - диф-ма на [a,b];
- диф-ма на [a,b]; 
 ; L: x=g(y);
; L: x=g(y); 
 ;
;
2).  ; x(t),y(t) – непрерывно диф-ма на
; x(t),y(t) – непрерывно диф-ма на  ; L:
; L: 

 ;
; 
3).  ;
;  ; L:
; L: 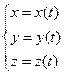


4).  ;
;  ;L:
;L:  ;
; 
 ;
;  ;
; 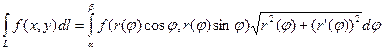
Билет 36.
Интеграл по ориентированной фигуре от векторной ф-ции.

Векторная ф-ция 3х переменных x,y,z, определенной на фигуре Ф. Ф-ции P,Q,R называются координатами  . Фигура Ф называется ориентированной, если в каждой ее точке М задан некоторый вектор
. Фигура Ф называется ориентированной, если в каждой ее точке М задан некоторый вектор  , характеризующий эту фигуру. Диния
, характеризующий эту фигуру. Диния  называется ориентированной, если на ней выбрано направление перемещения.
называется ориентированной, если на ней выбрано направление перемещения.
Гладкая поверхность называется двусторонняя, если нормаль к ней при обходе по замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, возвращается к своему первоначальному положению.
1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4). 
5).  ; n-я интегральная сумма для векторной ф-ции a(M) по ориентированной с помощью вектора P (n) фигуре Ф.; 6).
; n-я интегральная сумма для векторной ф-ции a(M) по ориентированной с помощью вектора P (n) фигуре Ф.; 6).  (*)
(*)
Если (*) существует, конечен и не зависит от способа построения интегральной суммы  , то он называется интегралом по орентированной фигуре Ф от векторной ф-ции a (M).
, то он называется интегралом по орентированной фигуре Ф от векторной ф-ции a (M).


P(x,y,z) Q(x,y,z) R(x,y,z) a =(P,Q,R)
Если ф-ции P,Q,R непрерывны на гладкой, ограниченной, содержащей граничные точки ориентированной фигуре Ф, то интеграл существует.
Частные случаи интегралов по ориентированной фигуре.
Свойства интеграла по фигуре от векторной ф-ции.
1).  ; 2).
; 2).  , c=const
, c=const
3).  ; 4).
; 4). 
Билет 4.
Понятие первообразной ф-ции и неопределенного интеграла.
Пусть ф-ция f(x) определена на X. Ф-ция F(x) – первообразная для f(x) на X, если F’(x)=f(x) для любого x € X.
F(x) – первообразная, F(x)+C – первообразная.

 для
для 
 ;
; 
Совокупность всех первообразных F(x)+C для ф-ции f(x), определенное на X, называется неопределенным интегралом от ф-ции f(x) на X и обозначается 
 ;
; 
Основные свойства неопределенного интеграла.
1). 
2). 

3). 
4). 

Билет 5.
Замена переменной в неопределенном интеграле.
Внесение множителя под знак диффиринциала.
Теорема: Пусть  определена и диф-ма на X. U- множество значений ф-ции
определена и диф-ма на X. U- множество значений ф-ции  . Для f(U) существует F(U) на U.
. Для f(U) существует F(U) на U.  Тогда для g(x) на X сущ-т первообразная
Тогда для g(x) на X сущ-т первообразная  , т.е.
, т.е. 
Док-во: 
На практике: 
Вынесение множителя из-под знака дифференциала.
Теорема: Пусть  определена и диф-ма на T.
определена и диф-ма на T.  на Т. Для g(t) на Т существует G(t).
на Т. Для g(t) на Т существует G(t).  , тогда для f(x) на X существует первообразная
, тогда для f(x) на X существует первообразная  .
. 
Док-во:  возрастающая
возрастающая  гарантировано
гарантировано  (обратная).
(обратная).

На практике: 
Билет 42.
Скалярные поля. Производная по направлению. Градиент.
Пусть V – некоторая область в пространстве. Говорят, что в этой области задано скалярное поле, если каждой т. 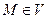 поставлено в соответствие некоторое число U(M) (пример – поле температур, освещенности). Скалярное поле не зависит от выбора системы координат. Поверхность или линия, на которой U(M) принимает постоянное значение называется поверхностью уровня скалярного поля.
поставлено в соответствие некоторое число U(M) (пример – поле температур, освещенности). Скалярное поле не зависит от выбора системы координат. Поверхность или линия, на которой U(M) принимает постоянное значение называется поверхностью уровня скалярного поля.
Пусть U(M) – некоторое скалярное поле.  - единственный фиксированный вектор.
- единственный фиксированный вектор.  -фиксированая точка.
-фиксированая точка.  ;
;  ;
; 
Если  , то он называется производной скалярного поля U(M) по направлению
, то он называется производной скалярного поля U(M) по направлению  в точке
в точке  .
. 
lnH-скорость изменения ф-ции U(m) по направлению  в точке
в точке  .
.
Не нашли, что искали? Воспользуйтесь поиском: