
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ограниченность ∫-ой ф-ции.
1.(необход.условие ∫-ти ф-ции). Если y=f(x) ∫-ма по Риману то она ограничена. f(x) € R[a,b] →сущ.М>0, |f(x)|≤M, для любых х€[a,b].
Д-во: предположим, что f(x) не огран. на [a,b] тогда при люб. разбиении τn найдется часть от k [xk-1,xk] на котором f(x) не ограничена. В этом случае можно выбрать εk€[xk-1,xk], таким обр, чтобы |f(εk)|>любого наперед заданного положит. числа, а это означ., что не сущ-ет конечного limx→0 Ssn
Следствия: если ф-ция неогр. то на неинтегрируема на [a,b]; огранниченность явл. лишь необход. условием инт-сти, но не достаточным.
ì 1, х – рацион.
D(x)= î 0, х – иррац.
D(x) – огр. на [0,1]
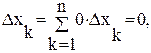
 εk-рац.
εk-рац.
εk-ирррац
D(x) – не инт. по Р., но она огр.
Теорема 1: f(x) непр. [a,b], то она явл. интегр.
Теорема 2: f(x) кусочно-непрер. на [a,b]
Ф-ция f(x) явл. кусочно-непрер. на [a,b], если она огранич. и непрер. на отр. [a,b] всюду, кроме конечн. числа точек разрыва 1-го рода.
Теорема 3: Ф-ция f(x) монотонная на [a,b] интегр. на [a,b] …
Билет 11
Св-ва опред. ин-ла.
1.  f(х)dх=0
f(х)dх=0
2.  dх=b – a; f(x)º1
dх=b – a; f(x)º1 
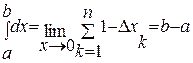
3.  f(х)dх= -
f(х)dх= - 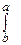 f(х)dх
f(х)dх
4. f(x)ÎR [a,b];  C f(х)dх=C
C f(х)dх=C  f(х)dх=
f(х)dх=
= 
5. f(x), g(x) Î R [a,b], то f(x)+g(x) Î R [a,b];  (f(х)+g(x))dх=
(f(х)+g(x))dх=  f(х)dх+
f(х)dх+  g(х)dх
g(х)dх
6. (аддитивность опред. ин-ла)
" a, b, c  f(х)dх=
f(х)dх=  f(х)dх+
f(х)dх+  f(х)dх
f(х)dх
7. Если f(x"хÎ[a,b], то  f(х)dх³0, a>b
f(х)dх³0, a>b  f(х)dх=
f(х)dх= 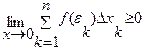
8. Монотонность опред. инт.: Если f(x), g(x)ÎR [a,b], f(x)£g(x) "xÎ[a,b], то  f(х)dх<
f(х)dх<  g(х)dх, a<b
g(х)dх, a<b
Док-во: g(x) – f(x)³0 "xÎ[a,b], 0£  (g(x) – f(x))dx=
(g(x) – f(x))dx=  g(х)dх -
g(х)dх -  f(х)dх
f(х)dх
9. Если f(x)ÎR [a,b], то |f(x)|ÎR [a,b]
|  f(х)dх |£
f(х)dх |£  |f(х)|dх
|f(х)|dх
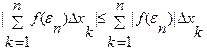
10. (Оценки опред. инт.): Если m и M – наимен. и наибол. зн. f(x) на [a,b], то m(b-a)£  f(х)dх£M(b-a)
f(х)dх£M(b-a)
m£f(x)£M; "xÎ[a,b]
m  dх £
dх £  f(х)dх£M
f(х)dх£M  dх
dх
m(b-a)£  f(х)dх£M(b-a), a<b
f(х)dх£M(b-a), a<b
11. Теорема о среднем: Если f(x) непр. на [a,b], то $ т. xÎ[a,b], что выполн. рав-во  f(х)dх=f(x)(b-a)
f(х)dх=f(x)(b-a)
Док-во: f(x) непр. на [a,b], m – min зн. f(x) на [a,b], M – max; "xÎ[a,b] m£f(x)£M; иссл. оценку ин-ла:
m(b-a)£  f(х)dх£M(b-a), b-a>0
f(х)dх£M(b-a), b-a>0
: (b-a) m£( f(х)dх) / (b-a))£M; l::=
f(х)dх) / (b-a))£M; l::=  f(х)dх) / (b-a)
f(х)dх) / (b-a)
найдется такая x, что f(x)=l,xÎ[a,b] =>  f(х)dх=f(x)(b-a) ч.т.д.
f(х)dх=f(x)(b-a) ч.т.д.
Билет 6.
Интегрирование по частям в неопределённом интеграле.
Т. Пусть функции U(x) и V(x) непрерывны на некотором промежутке X, дифферинциируемы в его внутренних точках и на Х существует 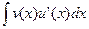 , тогда
, тогда
На Х существует 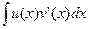 , причем
, причем 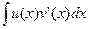 = u(x)v(x)-
= u(x)v(x)- 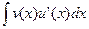 , или
, или
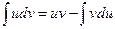 ;
;
Док-во:
d(uv)=vdu+udv; 

Билет Интегрирование рациональных функций.
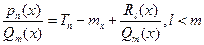
Интеграл от многочлена – легко и просто. Правильная рациональная дробь раскладывается на сумму элементарных дробей.
Типы дробей:
1)  , 2)
, 2) 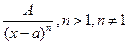 ,3)
,3)  ,4)
,4) 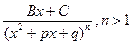
1) 
2) 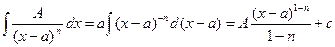
3)

4) 
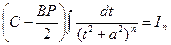 - рекуррентная формула
- рекуррентная формула
Вывод: интеграл от любой рациональной ф-ции выражается элементарной ф-цией ln,arctg, степенная.
Билет 37.
КРИ-2
Механический смысл КРИ-2:
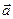 (М) – вектор силы; L=AB; Работа силы по перемещению вдоль L. Если
(М) – вектор силы; L=AB; Работа силы по перемещению вдоль L. Если 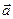 (М) – переменная сила, а AB – кривая, то:
(М) – переменная сила, а AB – кривая, то: 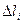 - настолько малы, что перемещение на кусочек по направлению совпадает с единичным касательным вектором.
- настолько малы, что перемещение на кусочек по направлению совпадает с единичным касательным вектором. 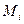 -произвольная точка.
-произвольная точка. 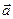 (
(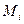 ) – постоянная сила.
) – постоянная сила. 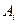 =(
=(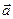 (
(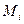 ),
), 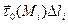 )=(
)=(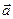 (
(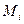 ),
), 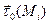 )
) 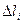
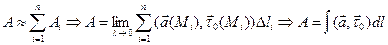
!!! С механической точки зрения КРИ-2 представляет собой работу силы вдоль линии L.
Скалярная форма КРИ-2
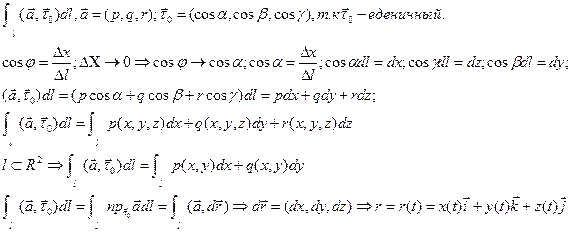
Вычисление КРИ-2
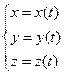 ,
, 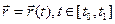
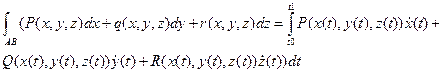
Не нашли, что искали? Воспользуйтесь поиском: