
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ И ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
ОБЩИЕ УКАЗАНИЯ
Контрольная работа № 1 по разделу курса - проекционное черчение включает 3 задания, которые выполняются студентами на трёх форматах A3 карандашом с помощью чертёжных инструментов по государственный стандартам трёхсотой группы (ГОСТ 2.300 - 68). Основная надпись должна быть оформлена по ГОСТ 2.104 - 68.
1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ НА ПЛОСКОСТИ
Задание № 1 по инженерной графике связано с геометрическими построениями на плоскости и выполняется (см. рис.1) с учетом общих правил геометрического конструирования фигур и единого оформления чертежа, предусмотренных ГОСТ 2.301-307-68,81. Поскольку объектом рассмотрения являются двумерные (плоские) фигуры, изображаемые на плоском чертеже, то для выполнения работы не требуется знаний раздела курса "Проекционное черчение". Напомним, что в последнем изучаются правила построения изображений трехмерных (объемных) фигур на плоскости чертежа.
В задании № 1 необходимо выполнить:
1. Геометрический анализ плоской СФ с целью выявления составляющих ее НФ;
2. Построение НФ, заданных полным и неполным набором параметров с учетом геометрических условий;
3. Построение точек сопряжения НФ и выполнение самих сопряжений;
4. Рациональное базирование фигуры (задание базовой СК) и определение минимального достаточного количества проставляемых размеров с учетом геометрических условий взаимоотношений НФ в СФ.
Перечисленные задачи решаются с помощью теории параметризации [1,2], как единой методической базы, отвечающей на основные вопросы формирования и чтения чертежа любой фигуры (плоской либо пространственной).
Задание выполняется на формате A3 (420 х 297 мм). Все построения сохраняются, являясь тонкими линиями (~ 1/3 S), где S - основная контурная линия. Каждая точка сопряжения должна быть построена пересечением двух линий - контура фигуры и одной из линий построения. Размеры проставляются по мере выполнения геометрических построений, как это рекомендовано в разделе 1.3.
Геометрические построения на чертеже можно проводить с помощью простейших чертежных инструментов (циркуля, линейки, угольника) на формате чертежной бумаги, а также на экране ПК с помощью набора команд с клавиатуры и устройства типа "мышь"
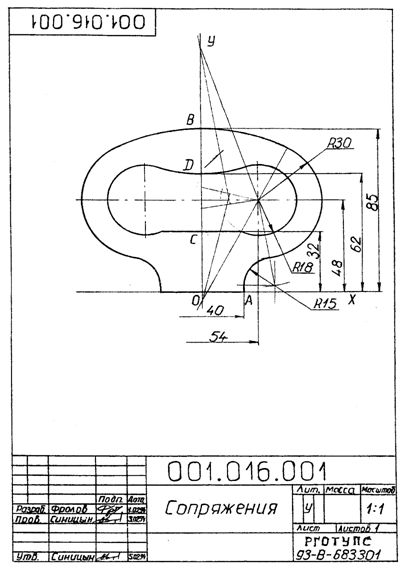
Рис.1
При этом алгоритмы геометрических построений и в том, и в другом случаях одинаковы и включают последовательность некоторых графических операций построения вспомогательных элементов сопряжения НФ в структуре СФ [2].
К элементарным геометрическим построениям относятся графические операции, связанные с делением отрезка прямой на заданное число равных частей, построением и делением углов на равные части, проведением параллельных и перпендикулярных прямых, делением окружностей и построением правильных многоугольников и т.д. Перечисленные алгоритмы описаны в [3] и могут быть при необходимости дополнительно изучены студентами. Рассмотрим более подробно нетривиальные алгоритмы геометрических построений, необходимые для выполнения первого задания контрольной работы.
1.1. ОСНОВНЫЕ ГРУППЫ АЛГОРИТМОВ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Первая группа алгоритмов связана с построением точек взаимного сопряжения двух окружностей и сопряжения двух окружностей прямой при заданных радиусах и координатах их центров.
1.1.1. Сопряжение двух окружностей (рис.2), заданных пятью параметрами (П-5). Наборы параметров могут быть различными, например, 4ПП - координаты двух центров и 1ПФ - радиус, или ЗПП и 2ПФ. Алгоритм построения точки сопряжения основан на построении линии центров окружностей и отыскании на ней точки касания с засечкой одним из радиусов (R1 Ú R2). Алгоритм построения реализуется независимо от характера касания -внешнего либо внутреннего.
1.1.2. Сопряжение двух окружностей прямой. Представленная на рис. 3 СФ обычно задается параметрическим числом 6П (4ПП + + 2ПФ), связанным с окружностями, и геометрическим условием касания (внешнее, внутреннее), воспринимаемым с чертежа "на глаз".
1.1.2.1. Внешнее касание связано с построением точек А и С. Алгоритм построения: в С1 строим окружность радиуса (R1 – R2) и точку G (0,5С1С2); из точки G -строим половину окружности радиуса R = 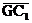 =
= 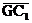 ; получаем точку L; C1L продолжаем до пересечения с окружностью радиуса R1, получаем искомую точку А; проводим С2С||С1А и получаем вторую искомую точку С.
; получаем точку L; C1L продолжаем до пересечения с окружностью радиуса R1, получаем искомую точку А; проводим С2С||С1А и получаем вторую искомую точку С.
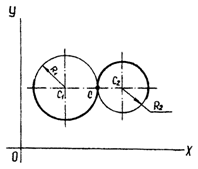

| Рис.2 | Рис.3 |
1.1.2.2. Внутреннее касание связало с построением точки В и D аналогично случаю внешнего касания. Отличие заключается в построении в центре C1 вспомогательной окружности суммарного радиуса (R1 + R2). Дальнейшая часть алгоритма аналогична приведенной выше (рис.3).
1.1.2.3. Частным случаем алгоритма (1.2.1) является задача проведения касательной к окружности (ЗП) из данной точки (2П) - рис.4, 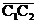 =
=  .
.


Рис.4 Рис. 5
Вторая группа алгоритмов связана с построением сопряжений двух прямых окружностью заданного либо неизвестного радиуса при фиксированной точке на одной прямой. Данная система имеет параметрическое число 5П (4ПП+1ПФ).
1.2.1.Сопряжение двух прямых окружностью заданного радиуса R (рис.5). Из произвольной точки прямой а восстанавливаем перпендикуляр (h ^ а), на котором откладываем отрезок AD = R (заданный радиус). Проводим прямую l || a. Аналогичные построения повторяем для прямой b. Из точки О опускаем два перпендикуляра на прямые а и b. Точки К и N являются искомыми точками сопряжения прямых а и b окружностью радиуса R с центром О.
1.2.2. Сопряжение двух прямых (n, m) дугой окружности в заданной точке Е одной из прямых (рис.6).

| Рис. 6 | Рис. 7 |
Строим биссектрису l угла, составленного заданными прямыми. Из точки Е восстанавливаем перпендикуляр до пересечения с биссектрисой l. Точка С1 является центром сопрягающей окружности. Точка В получена тривиальными построениями.
Третья группа алгоритмов для решения наиболее сложных задач на построение точек сопряжения и центров окружностей с нетривиальными исходными данными.
1.3.1. Задана точка А окружности 01 (рис.7). В точке А задано направление диаметра, то есть определен один параметр положения. Вторая окружность 02 полностью определена (ЗП). Требуется построить сопряжение окружностей. Касание внутреннее.
Решение. Из точки А на оси ОХ откладываем отрезок АВ = r2. Из центра отрезка C2В проводим перпендикуляр до пересечения с осью ОХ. Точка пересечения С1 есть центр окружности 01. Проводим линию
центров С1 С2. Строим точку Е - точку сопряжения двух окружностей.
При построении точки сопряжения двух окружностей внешнего касания (рис.8) точку В строим справа от точки А. Остальная часть алгоритма не меняется.
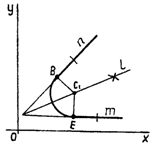
1.3.2. Внешнее сопряжение двух заданных окружностей 01,02 третьей, заданной одним параметром формы r3, - рис.9.


| Рис. 9 |
| Рис 8 |
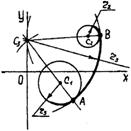
Решение. Из заданных центров окружностей C1,C2 строим дуги суммарных радиусов (r1+r3) и (r2+r3). На их пересечении строим центр окружности 03.Точки сопряжений А и В лежат на линиях центров С1С3, С2,С3. При внутреннем сопряжении центр С3 строим на пересечении радиусов (r3- r1) и (r3 - r2) – рис.10.
|
|
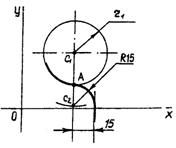
1.3.3. Ряд алгоритмов связан с построением параметров сопряжения попарных окружностей, заданных различными наборами параметров и геометрическими условиями, например сопряжение, представленное на рис.11.
1. 2. АНАЛИЗ ЗАДАНИЯ И ПОРЯДОК ЕГО ВЫПОЛНЕНИЯ
Каждому варианту задания соответствует геометрическая фигура - плоский контур, составленный из НФ. Исходные данные представлены в таблице 1 вариантов (см. ниже).
Каждая строка таблицы содержит координаты опорных точек
контура A (x / y); B (x / y);... и параметров окружнос
тей либо их дуг 01; 02;... по схеме Хс /Yс; R... (Хс,Yс - координаты центра окружности; R...- радиус). Если какие-либо параметры окружности заданием не выявлены, то в соответствующей графе проставлены многоточия. Декартова система координат ОХY определена на каждом рисунке для задания исходных данных. Базовая система отсчета может не совпадать с исходной. Она выбирается студентами самостоятельно из условий минимизации количества параметров (размеров фигуры).
1.2.1. Порядок выполнения работы
1.2.1.1. Анализ фигуры по следующей схеме:
а) определение количества осей симметрии (одна или две);
б) оценка по результатам п.1,а половины или четверти фигуры;
в) выбор направления обхода данной части контура и вычисление количества параметров для каждой НФ с учетом геометрических условий.
1.2.1.2. Задание базовой системы координат на чертеже из условий минимизации числа параметров. В отдельных вариантах базовая система координат совпадает с исходной, в которой реализовано задание исходных данных.
1.2.1.3. Реализация алгоритма построения контура на формате. Все построения выполняются в базовой системе координат.
На поле чертежа по заданным координатам строятся опорные точки контура (А, В,...). Далее проводятся окружности, заданные полным набором параметров (ПП=2; Ш-I; П=3), и от-
резки прямых. Все построения выполняются в тонких линиях. Строятся сопряжения прямых и окружностей, а также попарные сопряжения окружностей, заданных неполными наборами геометрических параметров. Все линии построений сохраняются. Каждая точка сопряжения контура должна быть определена пересечением линий построения с контуром обвода фигуры.
1.2.1.4. Обводка контура фигуры (половины, либо четверти) сплошной линией толщиной S и отображение симметрично по заданным условиям (см.п.1,а).
1.2.1.5. Простановка размеров по мере построений. Их количество должно соответствовать параметрическому числу фигуры.
1.3. ОСНОВНЫЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
Формат A3 рекомендуется располагать длинной стороной горизонтально. В основной надписи (штампе) заполняются следующие графы:
1.4.1. Обозначение - прямым шрифтом Б10:
| · | · | |||||||||
| ¾ | ¾ | ¾¾¾ | ¾¾¾ | |||||||
| а | б | в | г |
Где а - первый курс; б - номер контрольной работы;
в - номер варианта задания; г - порядковый номер листа в контрольной работе.
1.4.2. Наименование - "Геометрические построения" или "Сопряжения". Надпись выполняется наклонным шрифтом А7 с заглавной буквы без кавычек.
1.4.3. Масштаб: 1:1 - шрифт А7 наклонный.
1.4.4. Фамилии преподавателя и студента записываются наклонным шрифтом произвольного размера.
1.4.5.Содержание остальных граф ясно из примера (см. рис. 1).
Все надписи выполняются с обязательной строчной (по высоте) разметкой. В случае необходимости выполняется разметка наклонными (вертикальными) линиями.
В дополнительную графу, расположенную в верхнем углу, записывается прямым шрифтом А7 обозначение чертежа в перевернутом положении.
Размеры проставляются наклонным шрифтом А5 на расстоянии 0,5-1 мм от размерных линий. Контур фигуры обводится сплошной основной линией толщиной S» 0,8-1 мм.
2. ПОСТРОЕНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА
При выполнении задания № 2 расчетно-графической работы по разделу "Инженерная графика" изучаются основные разделы теории чертежа - базирование объекта, выбор главного вида составной фигуры (СФ), построение минимального количества основных изображений, образмеривание чертежа. Единой методической базой для решения перечисленных задач является теория параметризации, основные положения которой изложены в методическом пособии [ 1,2 ].
При выполнении индивидуальных заданий, варианты которых представлены в табл. 2, студенты выполняют геометрический анализ составной фигуры, выделяя простейшие (непроизводные) фигуры (НФ) в ее составе, к таким НФ относятся: прямоугольные призмы (сплошные и с отверстиями); сплошные и полые цилиндры; конусы, сферы и т.д. Базирование каждой НФ в составной фигуре выполняется в основной (базовой) системе координат, жестко связанной с СФ. Правильное задание базовой системы координат (БСК) является первой наиболее важной задачей построения проекционного чертежа любого объекта. Методика выбора БСК изложена в пособии [2].
Анализ СФ включает исследование каждой НФ, результаты которых представлены в табл. 3. По результатам анализа вычерчивается главный вид составной фигуры. В проекционных связях строится минимальное необходимое количество основных изображений, проставляются размеры. Все размеры снимаются с наглядного (аксонометрического) чертежа-задания. Диаметры окружностей измеряются по сопряженным осям соответствующих эллипсов вдоль осей БСК. Изображения на чертеже увеличиваются в два раза (М 2:1). ГОСТ 2.302-68 [2, с.16-18]. Все отверстия считаются сквозными. Пример выполнения одного из вариантов задания 2 представлен на рис.18.
Таблица 2.
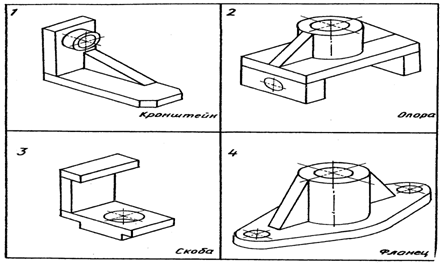

2.1. УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
В качестве примера рассмотрим фигуру, напоминающую СФ варианта 1.
Геометрический анализ целесообразно выполнять на черновике (клетчатой тетрадной бумаге).
Геометрический анализ фигуры (рис. 19) позволяет установить четыре непроизводные фигуры: 1 - прямая шестигранная призма; 2 - параллелепипед со сквозным цилиндрическим отверстием; 3 - прямая треугольная призма; 4 - цилиндр со сквозным отверстием. Большинство непроизводных фигур (1,2,4) имеют единую плоскость симметрии, с которой должна быть совмещена одна из координатных плоскостей БСК, например OZX [2 ]. По осям OХ и OZ реализуется пара габаритных размеров СФ, третий габаритный размер измерен вдоль оси
OY (рис.20). Названия осей заданы произвольно и могут быть изменены по результатам геометрического анализа фигуры. Напомним, что на главном виде координатные отрезки осей OZ и OX должны проецироваться в натуральную величину, а ось OY вырождается в точку (рис. 21).
Таким образом, первая задача - выбрать направление проецирования главного вида СФ и назвать соответствующим образом оси БСК. Зададим три направления проецирования:  ;
; 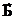 ;
;  ; (рис.20) и выберем из их числа единственное, соответствующее главному виду.
; (рис.20) и выберем из их числа единственное, соответствующее главному виду.
Выбор главного вида (пл. OZX) СФ осуществляется по следующему правилу [ 2 ]. Выбирается главный вид для каждой непроизводной фигуры (1, 2, 3, 4) в структуре СФ. Главный вид СФ соответствует наибольшему количеству главных видов непроизводных фигур (НФ).
Выбор главного вида НФ осуществляется по принципу реализации максимального количества параметров фигуры при проецировании на плоскость [2]. Выполним анализ четырех НФ в структуре СФ (рис. 19,20). Результаты анализа сведены в табл. 3.
| № НФ | Плоскость главного вида | Направление проецирования | Число реализованных параметров (с учетом ГУ*) | Главный вид СФ |
| OXY | 
| 4ПФ | OXZ

| |
| OXZ | 
| 5(3ПФ+2ПП) | ||
| OXZ | 
| 4(2ПФ+2ПП) | ||
| OXZ либо OXY | 
| 5(3ПФ+2ПП) |
Первая НФ (см. рис. 19, 20) проецируется по направлению  на плоскость OХУ максимальным числом параметров (4 параметра формы). Вторая НФ проецируется на плоскость OXZ по направлению
на плоскость OХУ максимальным числом параметров (4 параметра формы). Вторая НФ проецируется на плоскость OXZ по направлению  тремя параметрами формы (включая диаметр отверстия) и двумя параметрами положения оси отверстия над плоскостью ОХУ. Третья НФ проецируется также на плоскость OXZ по направлению
тремя параметрами формы (включая диаметр отверстия) и двумя параметрами положения оси отверстия над плоскостью ОХУ. Третья НФ проецируется также на плоскость OXZ по направлению  двумя параметрами формы и двумя – положения. Четвертая НФ – тремя параметрами формы и двумя – положения.
двумя параметрами формы и двумя – положения. Четвертая НФ – тремя параметрами формы и двумя – положения.
Из табл. 3 видно, что направление проецирования  является доминирующим, поэтому плоскость главного вида закрепляется за координатной плоскостью OXZ БСК. Если названия осей не соответствуют плоскости главного вида OXZ, то необходимо произвести их переименование, руководствуясь установленным направлением проецирования (направление
является доминирующим, поэтому плоскость главного вида закрепляется за координатной плоскостью OXZ БСК. Если названия осей не соответствуют плоскости главного вида OXZ, то необходимо произвести их переименование, руководствуясь установленным направлением проецирования (направление  в рассмотренном примере). Важно помнить, что положительные направления осей комплексного чертежа регламентированы ГОСТ 2.305-68 [2], поэтому кроме коррекции наименования осей возможно следует изменить и их направления на противоположные. Итак, главный вид СФ может быть построен при проецировании последней вместе с осями БСК на плоскость чертежа по направлению
в рассмотренном примере). Важно помнить, что положительные направления осей комплексного чертежа регламентированы ГОСТ 2.305-68 [2], поэтому кроме коррекции наименования осей возможно следует изменить и их направления на противоположные. Итак, главный вид СФ может быть построен при проецировании последней вместе с осями БСК на плоскость чертежа по направлению  (см. рис. 18).
(см. рис. 18).
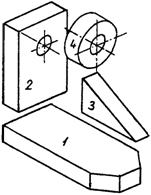

| Рис. 19 | Рис. 20 |
Основные изображения строятся в минимально необходимом количестве по принципу исчерпывающей реализации параметров размерного графа [1,2]. Однако в методику построения основных изображений может быть внесен формальный признак. Так, например, для определения геометрических свойств всех СФ, представленных в таблице вариантов заданий одного вида недостаточно, поэтому, не выполняя анализа реализации размерных параметров, на главном виде в рассматриваемом примере (рис. 18) построим второе основное изображение. Чтобы правильно его выбрать, снова воспользуемся данными табл.3, из которой следует, что по направлению проецирования  на плоскости ОХY (вид сверху) реализуется максимальное количество параметров (4ПФ) первой НФ. Итак, строим вид сверху, проецируя СФ на плоскость чертежа по направлению
на плоскости ОХY (вид сверху) реализуется максимальное количество параметров (4ПФ) первой НФ. Итак, строим вид сверху, проецируя СФ на плоскость чертежа по направлению  (рис.22), (рис. 18). Достаточно ли двух изображений для полного выявления геометрических свойств составной фигуры, покажет реализация ее геометрических параметров размерами.
(рис.22), (рис. 18). Достаточно ли двух изображений для полного выявления геометрических свойств составной фигуры, покажет реализация ее геометрических параметров размерами.
Образмеривание чертежа выполняется на основании параметрического анализа СФ, причем максимальное количество размеров группируется на главном виде. На остальных изображениях проставляются размеры только тех элементов, для выявления формы которых они были построены. Параметрический анализ фигуры нашего примера показывает, что с учетом геометрических условий СФ должна быть определена в заданной БСК 14-ю параметрами (размерами). На виде сверху (см. рис.18) проставляется один из габаритных размеров, пара размеров, определяющих форму основания прямоугольной призмы 1 и один размер - высота призмы 3. Остальные 10 размеров (в том числе пара габаритных) проставляются на главном виде. Построения изображений выполнены, размерный граф полностью исчерпан. Таким образом, для выявления геометрической формы СФ в нашем примере достаточно двух основных изображений - главного вида и вида сверху. Тема разрезы здесь не изучается, поэтому отверстие показано штриховыми линиями, условно.
2.2. ОФОРМЛЕНИЕ ЧЕРТЕЖА
Задание выполняется на формате A3 (420x297) и имеет стандартное оформление по ГОСТам 2.301-307.68,81 (см. рис. 18). Основная надпись выполняется по ГОСТ 2.104-68 [3., с.33-38]. В графе "Наименование" записывается с заглавной буквы название составной фигуры, указанное в таблице вариантов заданий, наклонным шрифтом А7. Обозначение чертежа записывается прямым шрифтом Б1O в основной надписи и шрифтом А7, также прямыми, в дополнительной графе (б левом верхнем углу поля чертежа) (см. раздел 1.4.). Графа масштаб содержит: 2:1. Прочая информация очевидна из чертежа-примера (см. рис.18).
Как уже отмечалось, геометрический анализ СФ целесообразно выполнять на черновике, формат A3 (рис.18) содержит: 1) аксонометрический чертеж или рисунок, выполненный от руки в глазомерном масштабе, фигуры задания с выбранной БСК, направлениями проецирования  ;
; 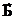 ;
;  и позициями непроизводных фигур (1, 2, 3, 4); 2) таблицу выбора главного вида фигуры (см. рис. 18 или табл. 3 в разделе 2.1); 3) комплексный проекционный чертеж составной фигуры с минимальным количеством изображений; 4) все размеры, реализующие параметрический граф составной фигуры (размерные числа наносятся шрифтом А5 наклонным).
и позициями непроизводных фигур (1, 2, 3, 4); 2) таблицу выбора главного вида фигуры (см. рис. 18 или табл. 3 в разделе 2.1); 3) комплексный проекционный чертеж составной фигуры с минимальным количеством изображений; 4) все размеры, реализующие параметрический граф составной фигуры (размерные числа наносятся шрифтом А5 наклонным).
3. ПОСТРОЕНИЕ ПРОЕКЦИОННОГО КОМПЛЕКСНОГО ЧЕРТЕЖА И АКСОНОМЕТРИИ
Задания № 3 контрольной расчетно-графической работы по инженерной графике (проекционное черчение) не связаны с выбором главного вида, оценкой минимального числа основных и дополнительных изображений объекта, образмериванием чертежа. Эти вопросы были рассмотрены при выполнении задания 2 по исходным данным, представленным наглядным (аксонометрическим) изображением предмета.
Здесь исходные данные представлены полной геометрической информацией на комплексном чертеже - двумя основными проекциями фигуры (горизонтальной и фронтальной). Внутренние (невидимые) поверхности обозначены штриховыми линиями. Содержание графической работы связано с умением прочитать чертеж, то есть мысленно восстановить форму объекта по двум его изображениям, построением разрезов для выявления формы внутренних поверхностей, сечения фигуры плоскостью общего положения, а также ее аксонометрического изображения (изометрии). Для контроля знаний, связанных с выявлением формы объекта по комплексному чертежу, необходимо построить проекцию объекта (вид слева) и выполнить разрез по правилам, предусмотренным ГОСТ 2.305-68. Такая задача носит исключительно контрольный характер и не связана с корректным построением комплексного чертежа объекта, для задания которого вполне достаточно двух основных изображений, представленных в табл. 4.
Перечисленные задачи решаются на основе геометрического анализа составной фигуры, с основными положениями которого познакомились, выполнив задание.
2. Варианты для выполнения заданий 3 представлены в табл.4. Десять вариантов соответствуют последней цифре номера зачетной книжки (студенческого билета). Предпоследняя цифра того же номера определяет дополнительные данные в соответствующей графе вспомогательной таблицы, расположенной под чертежом задания каждого из десяти основных вариантов.
Пример выполнения задания 3 на формате A3 представлен на рис. 23. Каждый фрагмент чертежа связан с решением некоторой графической задачи на основе правил проекционного черчения и положений ГОСТ 2.305-68. Рассмотрим основные этапы последовательности выполнения задания на примере одного из вариантов.
Не нашли, что искали? Воспользуйтесь поиском: