ПОСТРОЕНИЕ СТАНДАРТНОЙ АКСОНОМЕТРИИ

Для построения аксонометрии (наглядного изображения) фигу­ры используется ее комплексный чертеж - два исходных изобра­жения, определяющих полную геометрическую информацию о пред­мете, и заданные на них проекции базовой системы координат, жестко связанной с самим предметом. Третье, построенное изоб­ражение, может быть использовано для вспомогательных разъяс­нений формы той или иной линии, воспроизводимой на аксономет­рическом чертеже.

Определим основные этапы построения аксонометрии.

1. Успех построений определяется правильным заданием осей на комплексном и аксонометрическом чертежах, поскольку они являются проекциями единой базовой системы (рис.30). Стан­дартная изометрия (М_А 1,22:1) предусматривает углы между ося­ми 120° и их наименование, соответствующее рис. 30, г.

2. Построение выполняется по результатам геометрического анализа фигуры (см. раздел 3.1):

а) Строится призма 1. Каждая вершина рассматривается как точка, координаты которой переносятся с комплексного чертежа (X, Z - с рис. 30, а, Y - с рис. 30, б). Например, точка 1 (1₁; 1₂) (рис. 30, а, б) расположена в координатной плоскости XOZ, поэтому ее координата Y₁ - 0. Напомним, что приведенная изометрия предусматривает перенос координат с комплексного чертежа на аксонометрический без их пересчета, то есть каждый координатный отрезок измеряется на рис.30, а, б и откладывается вдоль соответствующей оси на аксонометри­ческом чертеже (рис. 30):

б) строится круговой цилиндр 2. Цилиндр ограничен двумя окружностями, которые изображаются в плоскости O'X'Y' и па­раллельной ей на высоте призмы. Следует правильно эадать нап­равления большой и малой осей эллипсов [2,3]. Большая ось эллипса равна 1,22 d окружности, малая - 0,71 d. Центры эл­липсов расположены в точках 2 и , которые строятся на аксо­нометрическом чертеже по общим правилам (2'; );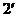

в) строится круговой цилиндр 3. Здесь строится один эл­липс от окружности, расположенной в плоскости OXZ с центром в точке 3 (3₁; 3₂) (рис. 30, а, б). Ось цилиндра параллельна оси OY, малая ось эллипса ей параллельна. Если с одной сто­ны цилиндр 3 ограничен окружностью, то с другой стороны его

завершают два эллипса (рис. 27), расположенных в плоскос­тях (1, 2) боковых граней приемы (рис. 26, б). Но эти построе­ния связаны уже со следующим этапом нашего алгоритма.

3. Строятся линии взаимного пересечения простых поверхнос­тей. К таковым относятся кривые.

а) начнем построения с эллипсов, на которых мы остановились выше. Относительно точки 4' (4₃;4₁) (рис.30, г) легко построить точки 5' (5₃;5₁) и 6' (6₃;6₁) (рис. 30, г), а также точки 7' (7₃;7₁) и 8' (8₃;8₁). Последние распо­ложены в плоскостях боковых граней призмы 1,2 соответственно (рис.25). Кроме точек 5', 6', 7', 8', необходимо построить в тех же боковых гранях еще по паре точек эллипсов,, например точки 9', 10,' 11,' 12'.

б) кривые (рис. 26) являются линиями пересечения двух цилиндров 2 и 3 (рис. 24). В аксонометрии эти линии стро­ятся аналогично способом переноса точек с комплексного черте­жа на аксонометрический с последующим их соединением плавной лекальной кривой. На рис. 30, г можно частично видеть кри­вую. Кривая в аксонометрии не видна.

4. Для выявления формы внутренних поверхностей и линий де­лается четвертной вырез фигуры, направленный в сторону наблю­дателя, плоскостями параллельными (совпадающими) координатным аксонометрическим O'X'Z' и O'Y'Z', на рис. 30, г такой вырез унич­тожил бы многие точки построений, необходимые для чтения и понимания изложенного алгоритма, поэтому ограничимся примером выполнения четвертного выреза, представленного на рис. 23.

5. Заполнение основной надписи.

В основной надписи (ГОСТ 2.104-68) заполняются графы:

разработал - фамилия студента;

проверил - фамилия преподавателя.

В графе "обозначение" записывается прямым шрифтом Б10 де­вятизначное число: (см. раздел 1.4).

Не нашли, что искали? Воспользуйтесь поиском: