
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исходная информация задачи
| Вид продукции | Нормы расхода материалов на единицу продукции | Обязательный минимум выпуска продукции | Прибыль от реализации единицы продукции | ||
| A | |||||
| Б | |||||
| В | Не лимитир. | ||||
| Г | Не лимитир. | ||||
| Ресурсы материалов | – | – |
Решение
Обозначим – количество единиц продукции вида А, Б, В, Г соответственно 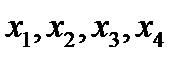 . Тогда математическую модель задачи можно записать следующем образом:
. Тогда математическую модель задачи можно записать следующем образом:
 ® max
® max
при условиях
 ;
;
 ;
;
 ;
;
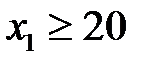 ;
; 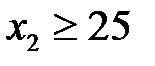 ;
; 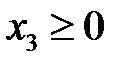 ;
;  .
.
Исходную информацию задачи переносим на рабочий лист Excel и применяем надстройку Поиск решения. В результате получаем численное решение задачи. На рис. 5 показаны рабочий лист, который в ячейках C6, D6, E6 содержит формулы: =СУММПРОИЗВ(C2:C5;K2:K5); =СУММПРОИЗВ(D2:D5;K2:K5); =СУММПРОИЗВ(E2:E5;K2:K5), а в ячейке I7 формулу: =СУММПРОИЗВ(I2:I5;K2:K5) (рис. 26-27).

Рисунок 26 - Рабочий лист

Рисунок 27 - Формула для ячейки I7
Таким образом, для получения максимальной прибыли из имеющихся ресурсов необходимо изготовить продукцию А в количестве 75 единиц и продукцию Б в количестве 25 единиц, остальные виды продукции производить нецелесообразно.
Задание № 2
Из деревянного бруса длины l = 6 м в количестве N = 100 шт. необходимо изготовить раму, содержащую следующие элементы:
брус длиной 1500 мм – 2 шт., 2000 мм – 2 шт., 2500 мм – 3 шт., 3000 мм – 2 шт.
Найти оптимальный план распила материала, чтобы количество отходов было минимальным при условии получения полных комплектов заготовки для рам.
Решение
Варианты распила бруса длины l = 6 м на заготовки приведены в табл. 18:
Таблица 18
Варианты распила бруса
| Вариант | Элементы распила бруса | Число реализаций варианта | ||||
| Брус 1500 мм | Брус 2000 мм | Брус 2500 мм | Брус 3000 мм | Длина остатка, м | ||

| ||||||
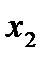
| ||||||
| 0,5 | 
| |||||

| ||||||
| 0,5 | 
| |||||

| ||||||

| ||||||

| ||||||
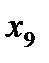
| ||||||
| 0,5 | 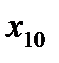
| |||||

|
На основании информации этой таблицы получим математическую модель задачи:

при условиях
 ,
,
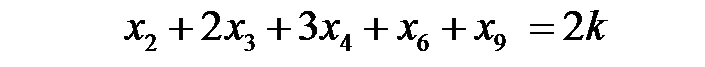 ,
,
 ,
,
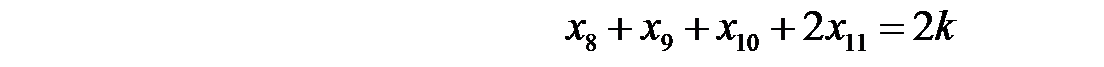 ,
,
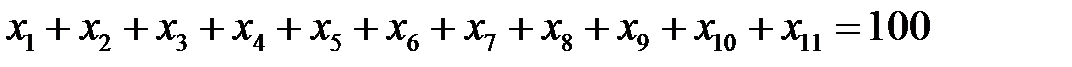 ,
,
 ,
,
где k – число комплектов для рам.
Для изготовления 14 рам понадобится 98 шт. бруса, из них 56 шт. необходимо распилить по варианту 6, 14 шт. по варианту 7 и 28 шт. по варианту 11. Минимальное количество отходов равно 14 м, это составляет 2,3% всей длины брусьев.
Задание № 3
Со сборочной линии предприятия в течение смены (8 ч) сходит 420 изделий. Контролер затрачивает на осмотр одного изделия 1,5 мин. Заработная плата контролера составляет 320 у. е. в месяц (при 22 рабочих днях). Издержки предприятия, вызванные несвоевременно выявленным браком, составляют 160 у. е. за одно изделие. Средний коэффициент брака на предприятии не более 0,4% от объема выпускаемой продукции. Требуется:
1) Найти оптимальное число контролеров для минимизации издержек предприятия.
2) найти число контролеров для повышения имиджа предприятия, при котором бракованный товар будет выявляться с вероятностью более 99% процентов.
3) Построить графики затрат, подтвердить расчет графически.
Решение
Содержательная постановка задачи состоит в следующем. Если изделие после сборки не подвергалось контрольному осмотру (все каналы были заняты и заявка получила отказ), то оно поступает на склад готовой продукции и оттуда направляется потребителю. Среди изделий, не проходивших контроль, могут оказаться и изделия с дефектом и браком. За отправку потребителю некачественной продукции предприятие штрафуется и, кроме того, несет дополнительные расходы, связанные с доставкой бракованных изделий от потребителей, устранением дефектов и доставкой их обратно потребителям. Чем больше в системе контролеров, тем выше вероятность обслуживания заявок и меньше возможность пропуска изделий с браком, но тем больше и издержки предприятия на содержание самой контрольной службы. Выберем в качестве критерия величину суммарных затрат предприятия на содержание контрольной службы и издержек, связанных с несвоевременно выявленным браком. Определим число каналов, которое обращает такой критерий в минимум.
Общие издержки предприятия определяются следующей формулой:
F (n) = (n · Зk + γ · K б · Зб · Р n) · T (52)
где n – число каналов в системе (контролеров);
Зк – затраты на содержание одного контролера в единицу времени;
γ – средний коэффициент брака;
К б – среднее относительное количество бракованных изделий, характерное для данного производства или для данного предприятия;
Зб – средние суммарные затраты предприятия, связанные с пропуском брака в изделиях;
T – множитель, изменяет только общую величину издержек, но не влияет на характер изменения критерия.
Первое слагаемое функции возрастает с ростом числа каналов n, а второе достаточно быстро и нелинейно падает в соответствии с поведением величины, стремясь к нулю. Сумма таких двух слагаемых всегда имеет минимум, который отвечает оптимальному числу каналов.
Для наглядности поведения функции можно выполнить графическое изображение, задаваясь рядом значений n = 0, 1, 2 и т. д. Далее из таблицы значений функции и графика ее поведения определяется оптимальное число каналов.
Для решения задачи необходимо произвести промежуточные расчеты и определить параметры, представленные в табл. 14.
Таблице 19
Не нашли, что искали? Воспользуйтесь поиском: