
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Корреляционный анализ. Это раздел мат.статистики ,изучающий взаимосвязи м/у изменяющимися величинами в изм
Это раздел мат.статистики,изучающий взаимосвязи м/у изменяющимися величинами в изм. ср. величины одной из них в зависимости от знач. другой.
Корреляция – соотношение.
Силу и тесноту взаимосвязи м/у изм-ся величинами изуч.кор. анализ,к-й рассм. связи м/у 2 факторами (парная кор) и м/у многими переменными (множест. корр)
о наличии или отсутствии кор.связи судят по кор полям.
Парная корр. вычисляется:
 (1)
(1)
 (2)
(2)
=  =
= 
если  =
=  ,то превращ. в дисперсию
,то превращ. в дисперсию
к-ты корр. -1 до 1
если  0 - с увелич. х,y уменьш.
0 - с увелич. х,y уменьш.
r=0- отсут. связь
значимость коэф. корр. м/о проверять,срав. с табл. знач. или по критерию стьюдента.
обычно если для всех k-переменных м/о вычислить матрицу парной корр.
D= 
эти коэф. м/о исп-ть при построении ур-я многих переменных.
также м/о вычислить к-ты множественной корр.,служащие для оценки качества предсказания:
R= 
 – дисперсия ср.
– дисперсия ср.

0 

если объем выборки небольшой,величину R неоход. корр-ть на систематич. ошибку:
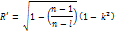
l – число коэф. ур-и регресс.
Значимость коэф. м/о проверить по критерию Стьюдента
D=  -множест. коэф. детерминации,показывает какая часть дисперсии ф-и отклика y объясн-ся
-множест. коэф. детерминации,показывает какая часть дисперсии ф-и отклика y объясн-ся
вариацией лин. комбинации выбран. факторов x1,x2........xk.
если  , то на 94% вариация результ. признака зависит от вариации выбран. факторов.
, то на 94% вариация результ. признака зависит от вариации выбран. факторов.
Построение точечных и интервальных оценок МО,дисп-и коэф.кор-ии(з-н распред)
Оценки полученные по выборке,яв-ся СВ.К оценкам обычно предъяв. требования состоятельности и несмещенности.
 , наз-ся состоят.,если с увелич.объема выборки n она стремится по вер-ти и оценки параметра a.
, наз-ся состоят.,если с увелич.объема выборки n она стремится по вер-ти и оценки параметра a.
Эмпирич.(выборочные) оценки явс-ся состоят-ми оценками теоритич. моментов,к-х не знаем.
Оценка наз-ся несмешанной, если ее МО при любом объеме выборки n равно оценив. парам-ру,т.е.
М[ 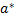 ]=a
]=a
Важнейшими хар-ми СВ яв-ся моменты СВ.
Первый нач. момент(ср. знач. МО):
М[x]=  =
= 
харак-т знач-е,вокруг к-го группируются все его возмож. знач-я,т.е. это ср.знач.
Второй централь. момент(дисперсия):
D[x]=  =
= 
хар-ет рассеивание (откл) СВ относит. ср. знач. Это мера откл. от ср. знач. Чем больше дисперсия,тем хуже МО хар-т выборку.
М/у СВ сущ-т связь,при к-й с изм. одной величины,меняется распред.др. Такая связь наз-ся стохастической. Для оценки тех или иных сторон стохаст. связи сущ. различ. показатели.
Важнейш. из них яв-ся коэф. корреляции.
Введем такую величину:
М[(x-  )(y-
)(y-  )]= cov (xy),
)]= cov (xy),
наз-ся корр.моментом (ковариацией) СВ x и y.
Безразмер. величина  - коэф. корр.
- коэф. корр.
 =
= 
Для независимых СВ  =0, а
=0, а 
если = 1,величина лин.зависима
f(x)- плотность вер-тей диф.ф-ла распред.
По выборке можно вычислить выбороч. хар-ки (оценки) МО-среднего,к-та коррел.,дисперсии по ф-лам:
 =
=  – средняя(1)
– средняя(1)
 - дисперсия(2)
- дисперсия(2)
 -к-т корреляции(3)
-к-т корреляции(3)
яв-ся СВ,их откл. от ген-х(погрешности) также будут случ.
М/о указ.лишь вер-ть той или иной погрешности.Для этого в мат.стат-ке исп. доверит. интервал и доверит.вероятности.
Имеется выборка объема n.
необход. оценить возмож.при этом ошибку для ген.парам.
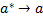 , при этом назнач.достат.большая вероятность
, при этом назнач.достат.большая вероятность  (довер.вер-ть),такая что события с вер-ю
(довер.вер-ть),такая что события с вер-ю  счит-ся достовер.
счит-ся достовер.
т.е.:
P  (4)
(4)
 - погреш-ть вычисления
- погреш-ть вычисления
P= 1-  –ур-нь значимости
–ур-нь значимости
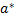 -
-  +
+  - доверит.интервал(5)
- доверит.интервал(5)
P  =
= 
Закон распред. величины  зависит от з-на распред. СВ х, для к-й вычисл.
зависит от з-на распред. СВ х, для к-й вычисл.  , в частности и от самого парам. a.
, в частности и от самого парам. a.
Исп-ся 2 метода:
1)приближ. подход,если знач. n≥50,то выражение для  неизвест. парам. замен-ся их оценками,т. е. (1),(2),(3).
неизвест. парам. замен-ся их оценками,т. е. (1),(2),(3).
2)от СВ  переходит к др. СВ з-н распред. к-й не завис. от оцениваемого парам.,a зависит только от объема выборки n и от вида з-на распред. СВ х.
переходит к др. СВ з-н распред. к-й не завис. от оцениваемого парам.,a зависит только от объема выборки n и от вида з-на распред. СВ х.
При небольших объемах выборки n,исп. распред. Стьюдента,можно записать:
 −
− 
 ≤
≤  ≤
≤  +
+ 
 (7)
(7)
здесь  -квантирью распред. Стьюдента при ур-не знач-ти t и степени свободы f=n-1
-квантирью распред. Стьюдента при ур-не знач-ти t и степени свободы f=n-1
Для дисперсии справедлива ф-ла:
 (8)
(8)
Не нашли, что искали? Воспользуйтесь поиском: