Программирование циклических алгоритмов с заданным

Числом повторений

Оператор цикла с счетчиком:

for (<выражение1>; <условие выполнения>; <выражение2>) <оператор>;

где <выражение1> - это выражение инициализации цикла (может содержать несколько операторов, разделенных запятыми);

<выражение2> - изменение параметра цикла (не обязательно целое).

Пример 1. Вычислить сумму элементов s=1+1/4+1/9+1/16+....

На основе анализа изменения параметра знаменателя определим алгоритм решения за­дачи (pис. 3) и напишем программу:

#include <stdio.h>

#include <conio.h>

void main ()

{

float s = 0, r;

int i,N;

clrscr(); //очистка экрана

printf ("\n Введите N ");

scanf ("%d",&N);

for (i=1; i<=N; i++)

{

r = 1.0/ (i*i);

s+ = r; // s = s + r

}

printf ("Сумма = %6.2f\n ",s);

getch();

}

Пример 2. Вычислить значения двух функций F1(x) = tg(x) и F2(x) = sin(x) в n точках, рав­номерно распределенных на интервале a ≤ x ≤ b, где a = -π/4, b = π.

Для реализации первого варианта данной задачи разработана СА (pис. 4) и cледующая программа:

#include <stdio.h>

#include <conio.h>

#include <math.h>

# define b 3.1415

void main ()

{

float F1, F2, x, dx, a = - b/4; // dx - шаг изменения x

int i, n; // i - переменная цикла

clrscr(); // очистка экрана

printf ("Введите число точек \n");

scanf ("%d", & n);

dx = fabs(b-a)/(n-1);

x = a;

printf (" ___________________ \n");

printf ("| I | X | F1 | F2 | \n");

printf ("|---|--------|--------|--------|\n");

for (i=1; i<=n; ++i) // оператор цикла

{ F2 = sin(x);

F1 = tan(x); // вычисление tg x

printf (" |%3d| %8.3f |%8.4f| %8.4f|\n", i, x, F1, F2);

x=x+dx; // x += dx

}

printf (" ____________________ \n");

getch();

}

Если точки не нумеровать, можно в цикле применить параметр х и шаг изменения dx. Тогда во втором варианте программы оператор цикла имеет вид: for (x = a; x <= b + dx / 2; x+ = dx) {... }

Задание 1 ( программа 3_1)

Для заданных с клавиатуры значений переменных x и n вычислить

1. X = 1 + 1/2 + 1/3 +... + 1/10. 2. Z = 2^. 4^. 6^. 8^.... ^.20.

3. Y = -x + 4x - 9x +... - 81 x.. 4. Y = x + x/3 + x/5 +... + x/17.

5. Y = n! = 1^. 2 ^. 3 ^....^.n. 6. Y = 1 - 3 + 3² - 3³ +... + 3¹⁰.

7. Y= x²/(2i-1). 8. Z = (x+i)/i. 9. Y= x²/i.

10. Y = 1 + x/2 + x²/4 + x³/6 +... + xⁱ/2i +... + x⁹ /18.

11. Y = 1 + x²/1! + x⁴/2! + x⁶/3! + … + x²⁰/10! = 1 + x²ⁱ/i!.

12. Y = 1 - x +x³/3! -x⁵/5!+...+(-1)ⁿ x^2n-1/(2n-1)!+... +x¹¹/11!.

13. е = 1 + 1/1! + 1/2! + ... + 1/n! +... (сравнить результат со значением функции EXP(1), определенной в Паскале).

14. π = 4(1-1/3+1/5-1/7+…+(-1)ⁿ/(2n+1)+…) (результаты сравнить с определенным в языке Паскаль числом Pi).

15. Y = arctg x = x - x³/3 + x⁵/5- ... + (-1)ⁿ x²ⁿ⁺¹/(2n+1)+... (|х|<1).

16. Z = LN(1+x) = x - x²/2 + x³/3 - ... + (-1)^n-1 xⁿ/n ^+... (|x|<1).

17. S = x - x³/3! + x⁵/5! - ... +(-1)ⁿ x²ⁿ⁺¹/(2n+1)! +....

18. Вычислить суммы положительных и отрицательных значений функции z = cos(nx + a) sin(nx-a), где n = 1,2,...,5, a и x - вещественные числа.

19. Вычислить сумму четных и сумму нечетных чисел натурального ряда до N.

20. Найти сумму факториала M= 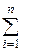i!.

Задание 2 (программа 3_2, программа 3_3)

Вычислить значения двух функций в n равномерно распределенных в диапазоне а≤x≤b точках. Результаты оформить в виде таблицы.

№ п/п	a	b	n	F1(х)	F2(х)
	-1 -2 - -1 -4 -	2 2		sin x cos x 1+2x+5 4e-|x|-1 | x+10|5 2 sin 2x +1 2-cos x 2-x/100 x3e2x 1/(1+ ) 5-3 cos x |sinx|+|cosx| e-x+cos2x e-x lg x cos x/2 2x lg x - 3x lg x 3-x/50 e2x - sin x 2x arctg x - 5	sin x + cos x -1 (x-1)3 cos x e-(x+5) (x+5)3 (1+sin2x) 20/(1+x2) ex sin x x ln2 x 2x/(1-4x) |sin x| - |cos x| e -2x x + sin x + e -x ctg x x e -x +ln x 10/(2+x2) e axx е2x lg x - 33x

Лабораторная работа 4

Не нашли, что искали? Воспользуйтесь поиском: