
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Переведення числа з 16-ої СЧ у 10-ну СЧ
Тепер згідно з завданням виконаємо переведення числа 5DB.E3816 з 16-ої систему у 10-ну способом Горнера, який завдається формулою:
Для цілої частини:
AN = (((ap-1N + ap-2)N... + a2)N + a1)N + a0
Для дробової частини:
AN = ((((a-1N + a-2)N... + an-1)N + a-l)N-n
Цілачастина:
1 2
5DB 16= (5*16+13)*16+11 = 149910
Переведення виконуємо крок за кроком, дії у дужках виконуємо за порядком (як вони пронумеровані).
1)9310
2)149910
5DB 16 = 149910
Дрібна частина:
1 2 3
0.E3816=((14*16+3)*16+8) *16-3 ≈ 0.88810
1)22710
2)364010
3) ≈ 0.88810
0.Е3816≈ 0.88810
Отже остаточно маємо, що число 5DB.E3816 у десятичній системі має наступний вигляд:
1499. 888
Ми можемо спостерігати, що кінцевий результат трішки відрізняється від початкових – це зумовлено ти, що вимірювання кількома способами впливає на точність.
Завдання 2
Перевести числа А, В, С в двійкову СЧ.
А – квадрат дня народження,
В – квадрат місяця народження,
С – 2 останні цифри року народження (взяти це число зі знаком мінус).
Обчислити S=А+В+С в десятковій системі числення.
Записати в прямому, зворотному та додатковому коді числа А, В, С.
Обчислити S2=А+В+C у цих кодах. Перевести S2 в десяткову систему
числення. Порівяти значення S2 та S.
Дата народження: 18.08.1997
У десятковій СЧ У двійковій СЧ:
A= 18*18= 324 = 101 000 1002;
B= 8*8= 64 = 10000002;
C= 1997= -97 = -11000012.
У десятковій СЧ:
S = A +B + C = 324 + 64 +(-97) = 291;
У двійковій СЧ:
S = A +B + C = 101 000 100 + 1000000 + (-1100001) = 1001000112;
Запишу в прямому, зворотному та додатковому коді числа А, В,С.
Прямий код:
Апр = 0.324 = 00.101 000 1002
Bпр = 0.64 = 00.10000002
Cпр = 9.97 = 11. 11000012
Зворотній код:
Азв = 0.324 = 00. 101 000 1002
Bзв = 0.64 = 00. 1000000 2
Cзв = 9.02 = 11. 00111102
Додатковий код:
Адод =0.324 = 00. 101 000 1002
Bдод = 0.64 = 00. 1000000 2
Cдод = 9.03 = 11. 00111012
Обчислю S2=А+В+C у прямому, додатковому та зворотньому кодах:
S2пр = 00.101 000 1002
+ 00.10000002
11. 1100001 2
11. 1111001012пр
S2зв = 00. 101 000 100 2
+ 00. 1000000 2
11. 0011110 2
11. 0000110102зв
S2дод= 00. 101 000 100 2
+ 00. 1000000 2
11. 0011101 2
11. 1101000012дод
При порівнянні кодів числа S2 та S, знаходжу:
S = -485 = 11. 1111001012пр =11. 1101000102зв = 11. 1101000012дод
S = S2 = S2зв =S2дод
Завдання 3
Задані 3 двійкових числа з плаваючою крапкою.
На малюнку 1 представлений формат числа.
| P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | a1 | a2 | ... | a24 |
| Порядок | мантиса |
Мал. 1. Формат числа
В таблиці 3 -знаки чисел А,В і С їхньої характеристики. Номер варіанта
для цієї таблиці обчислюється, як Nвар = Nсп mod4+1.
Таблиця 3
| № Варіант | Числа | Знак числа | Порядок |
| A B C | + - - | ||
| A B C | + - + | ||
| A B C | - + - | ||
| A B C | + + - |
Мантиса визначається як сума квадрата місяця і дня дати народження.
Обчислити результат операції R= А*В +C
Визначити абсолютну і відносну похибки результату.
Номер мого варіанта Nвар = Nсп mod4+1 = (12 mod 4) + 1 = 1
Тому:
Знак числа А - “ + ”, порядок - “ 2 ”.
Знак числа B - “ - ”, порядок - “ 3 ”.
Знак числа C - “ - ”, порядок - “ 5 ”.
Мантиса m = 8*8 + 18*18 = 38810 = 18416 = 1.84 * 162
Залишок
388/16 = 24 4(4)
388 = 18416
A = 1.84 * 162 = 42184000E
B = -1.84 * 163 = C3184000E
C = -1.84 * 165= C5184000E
Запись чисел у форматі:
A = 42184000E
0 7 32
| Порядок | Мантиса |
B = C3184000E
0 7 32
| Порядок | Мантиса |
C = C5184000E
0 7 32
| Порядок | Мантиса |
R = A * B + C;
Знайду A * B
0 7 32
P (порядок (A * B)) = M (мантиса(A * B)) =
01000100 1011000100*1111000100 = A6A1016
+ 01000010
- 01000000
Найдем сумму (A*B)+C:
(A*B)+C=(A6A1016 *165+1.8416*165)=
=165*(A6A1016+1.8416)=-A6A11.84*165= С584000E
Переведем числа A, B, C в 10 систему счислению, и сделаем соответствующие арифметические действия.
1. A=1.84*162=18416=38810;
2. B=-1.84*163=-184016=-620810;
3. C=-1.84*165=-18400016=-158924810;
4. A*B+C=-620810*38810-158924810=-399784210.
Переведем полученное нами число в 10 систему счисления:
(A*B)+C= С53D0100E=-A6A11.84*165=A6A118400016=-399795210.
Найдем абсолютную и относительную погрешность:
Rабс = D R = R - [R] = =-399795210 +399784210.= -11010
Rотн = ϬR = D R / [R] * 100% = -11010 / (-399784210)= 2.75%
Часть 2.
Задание №1 и №2
1) Находим номер варианта по формуле:

2) N=3.
3) Массив имеет 9 строк и 10 столбцов, адрес начального элемента равен 27.
4) Массив имеет вид
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | ||||
| # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
5) Найдем адрес элемента, который находится в 6 строке 8 столбце массива.
1. Развертка по строкам.
| ... | |||||||||||||||||||||
| # | # | # | # | # | # | # | # | # | # | # | # | ... | # | # | # | # | # | # | # | # | # |
a. Адрес элемента будем находить по формуле (отсчет с 0 и 1):
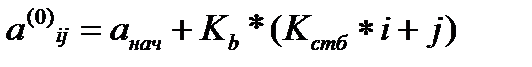

b. Kб=1байт: a(0)68=27+1*(10*6+8)=95.
c. Kб=2байт: a(0)68=27+2*(10*6+8)=163.
d. Kб=1байт: a(1)68=27+1*(10*5+7)=84.
e. Kб=2байт: a(1)68=27+2*(10*5+7)=141.
2. Развертка по столбцам
| ... | |||||||||||||||||||||
| # | # | # | # | # | # | # | # | # | # | # | ... | # | # | # | # | # | # | # | # | # | # |
a. Адрес элемента будем находить по формуле (отсчет с 0 и 1):


b. Kб=1байт: a(0)68=27+1*(9*8+6)=105.
c. Kб=2байт: a(0)68=27+2*(9*8+6)=183.
d. Kб=1байт: a(1)68=27+1*(9*7+5)=95.
e. Kб=2байт: a(1)68=27+2*(9*7+6)=163.
Задание №3
1) Находим номер варианта по формуле:

2) N=3.
3) Диапазон букв начала и конца:
a. N=3
b. M=12
То есть 9 букв алфавита, начиная с 3
1. Адрес вершины стека равен сумме адреса основания и количества элементов минус 1: 65+9-1=73
| В | |
| Г | |
| Д | |
| Е | |
| Ё | |
| Ж | |
| З | |
| И | |
| Й |
2. При помощи операции вытяжки из стека, мы получим элемент В. После вытяжки элемента из стека указатель будет указывать на букву Г. А указатель вершины будет равен 72.
3. Вставим в стек все буквы моего имени. Адрес вершины стека равен 82.
| А | |
| Л | |
| Е | |
| К | |
| С | |
| А | |
| Н | |
| Д | |
| Р | |
| В | |
| Г | |
| Д | |
| Е | |
| Ё | |
| Ж | |
| З | |
| И | |
| Й |
Задание №4
| Адрес | Указатель |
| А | |
| А-указатель 2 | |
| С – указатель 1 | |
| С | |
| Ш | |
| NULL | |
| Ш | |
| NULL |
Задание №5
1) Блок памяти может содержать 5 элементов.
2) Строим схему, которая показывает структуру циклической очереди.
G: 1) +A; 2) +B; 3) +C; 4) -; 5) -; 6) +G; 7) -.
| head | A | B | C | ||||
| body | A | B | C | ||||
| body | A | B | C | ||||
| body | A | B | C | G | |||
| tail | A | B | C | G |
Задание №6
1) Начало очереди 12, конец 22. (11 элементов)
2) При добавлении 4 элементов, значение начала равно 12, конца 26. (15 элементов)
3) При удалении 3 элементов, значение начала равно 15, конца 26. (12 елементов)
Задание №5
3) Блок памяти может содержать 5 элементов.
4) Строим схему, которая показывает структуру циклической очереди.
G: 1) +A; 2) +B; 3) +C; 4) -; 5) -; 6) +G; 7) -.
| head | A | B | C | ||||
| body | A | B | C | ||||
| body | A | B | C | ||||
| body | A | B | C | G | |||
| tail | A | B | C | G |
Задание №6
4) Начало очереди 12, конец 22. (11 элементов)
5) При добавлении 4 элементов, значение начала равно 12, конца 26. (15 элементов)
6) При удалении 3 элементов, значение начала равно 15, конца 26. (12 елементов)
Задание №7
Варіант 3

| A | ||||||||
| B | ||||||||
| C | ||||||||
| D | ||||||||
| L | ||||||||
| E | ||||||||
| K | ||||||||
| M | ||||||||
| N |
Обход дерева в прямом порядке:
ABDEKLСMN
Обход дерева в обратном порядке:
DKLEBNMCA
Обход дерева в симметричном порядке:
KELBDACMN
Не нашли, что искали? Воспользуйтесь поиском: