Равновесие в электрохимической цепи

Правильно разомкнутая электрохимическая цепь, на концах которой можно измерить электрическую разность потенциалов, всегда должна заканчиваться одинаковыми по своему химическому составу металлами (рис. 6.2, а). Обычно это достигается простым подключением к металлам медных проводов (рис. 6.2, б). Полную эквивалентность электрохимических цепей рис. 6.2, а и б) легко доказать, рассма-тривая в качестве переходной третью цепь (рис. 6.2, в). Включение между двумя металлическими проводниками третьего металлического провод-ника, согласно закону Вольта, не изменяет разно-сти потенциалов на концах цепи¹.

_________________________________________

¹⁾ Закон Вольта легко доказать, рассматривая электронные равновесия на границах двух мета-ллов и используя формулу (6.1.12).

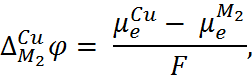
а на рис. 6.2, в

=

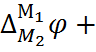
а б Сu Cu в Сu Cu

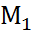
Рис. 6.2. Эквивалентные правильно разомкнутые эле- ктрохимические цепи. Пояснения в тексте.

Поэтому цепи на рис. 6.2, б и в эквивалентны. Но цепь на рис. 6.2, в одновременно эквивалент-на и цепи на рис. 6.2, а, так как отличается от неё двумя гальвани-потенциалами , которые компенсируют друг друга. Следовательно, экви-валентны также цепи на рис. 6.2. а и б, что и требовалось доказать.

Электрохимическая цепь является равно-весной при условии, что электрохимическое рав-новесие наблюдается на каждой фазовой грани-це, а разность потенциалов на концах цепи Е скомпенсирована разностью потенциалов от вне-шнего источника тока.

В качестве примера рассмотрим электрохи-мическую цепь, приведённую на рис. 6.3. Элек-тролитом в ней служит водный раствор соляной кислоты. Один из электродов представляет собой пластинку из платины, на которую электро-осаждением нанесена высокодисперсная пла-тина (так называемый платинированный плати-новый электрод). К поверхности этого электрода под атмосферным давлением подаётся газообра-зный водород, который адсорбируется на плати-не с образованием Второй электрод изгото-влен из металлического серебра, а его поверх-ность покрыта слоем плохо растворимой соли AgCl. Чтобы ионы серебра из раствора не попадали на второй электрод, на котором сере-бро будет осаждаться и затруднять адсорбцию водорода, в ячейку введена пористая перего-родка¹.

_____________________________

¹ На этой перегородке возникает мембранный потенциал, величина которого существенна в разбавленных растворах НСl.

Чтобы цепь заканчивалась одинаковыми по химическому составу металлами, к платиновому электроду присоединена серебряная проволока. Схема такой цепи Аg 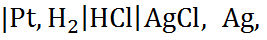где вертикальные чёрточки указывают границы фаз между двумя металлами или между металлами и раствором.

Разность потенциалов на концах этой цепи складывается из трёх гальвани-потенциалов:

E = 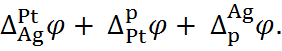(6.2.1)

Выражение для этих гальвани-потенциалов можно найти, рассматривая равновесия на каж-дой из фазовых границ. На границе I, где кон-тактируют серебро и платина, устанавливается равновесие

(6.2.A)

условием которого является

т.е.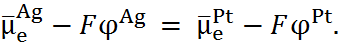

Следовательно,

. (6.2.2)

На границе II устанавливается равновесие

. (6.2.Б)

условие которого можно записать в виде

= ,

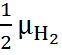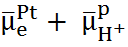т.е. 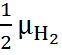= + F

Следовательно,

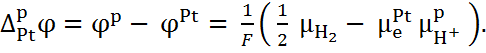(6.2.3) Наконец, на границе III существует равно-весие

AgCl + (6.2.B)

с условием

= ,

т.е. ,

а потому

=

(6.2.4)

После подстановки выражений (6.2.2)-(6.2.4) в уравнение (6.2.1) получаем:

E = =

= (6.2.5)

Поскольку изменение свободной энергии Гиббса для химической реакции

AgCl + 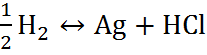(6.2.Г)

равно - уравнение (6.2.5) можно представить

в виде E =

Этот результат можно обобщить на любые химические реакции, которые осуществляются в электрохимической цепи при прохождении через неё не одного, а n электронов:

E = – (6.2.6)

Таким образом, разность потенциалов на концах равновесной электрохимической цепи однозначно связана с изменением свободной энергии Гиббса в ходе соответствующей химической реакции. Величина E, т.е. разность потенциалов на концах равновесной электро-химической цепи, называется её электро-движущей силой (ЭДС). Если же на отдельных фазовых границах (хотя бы на одной) равновесие не устанавливается, то разность потенциалов на концах цепи не равна ЭДС и уравнение (6.2.6) оказывается неприменимым. Величина nFE характеризует максимальную электрическую работу, которую можно получить при помощи электрохимической цепи. Уравнение (6.2.6) служит основой для расчёта различных электрохимических реакций.

При измерениях ЭДС нельзя пользоваться обычным низкоомным вольтметром, поскольку его включение в цепь нарушает равновесие из-за протекания значительного тока. Поэтому для измерения ЭДС применяют компенсационный метод, при котором разность потенциалов на концах цепи компенсируется выверенной по эталону разностью потенциалов от внешнего источника тока.

Ещё один метод определения ЭДС основан на использовании катодных вольтметров с очень высоким внутренним сопротивлением (R При включении в электрохимическую цепь такого вольтметра возникающий в цепи ток оказывается слишком малым, чтобы вызвать существенное отклонение от равновесия.

Знак ЭДС устанавливается по значению потенциала правого электрода относительно левого. Так, например, в рассмотренной цепи (см. рис. 6.3) справа находится серебряный электрод, потенциал которого положительнее потенциала серебряной проволоки, соединенной с платиновым электродом; поэтому E Рас-сматривая эту реакцию как процесс восстанов-ления хлорида серебра газообразным водородом, приходим к выводу, что Е когда окисленная форма исходного вещества (т.е. AgCl) находится у правого электрода, а восстановленная ( – у левого. Если бы в той же самой электрохи-мической цепи справа был помещён платиновый электрод, то ЭДС оказалась бы отрицательной. Но величина в таких условиях соответ-ствовала бы реакции

(6.2.Д)

которая самопроизвольно не протекает, т. е. для неё

Рассмотрим зависимость ЭДС от активностей отдельных компонентов на примере системы, приведённой на рис. 6.3. Компонентами этой системы являются газообразный водород, ионы водорода, ионы хлора, металлическое серебро и Химические потенциалы твердых веществ ( стан-дартным значениям

= и = const.

При условии, что водород подаётся к плати-новому электроду под давлением 1,01 Па (1 атм), = С другой стороны, для ионов водорода и хлора

+ RT ln и 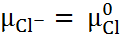+ RT ln .

Следовательно, уравнение (6.2.5) для ЭДС цепи можно переписать в виде

E = – (6.2.7)

где стандартное изменение свободной энергии Гиббса для химических реакций (6.2.Г); – стандартная ЭДС цепи.

Уравнение (6.2.7) – уравнение Нернста для ЭДС электрохимической цепи. Распространяя (6.2.7) на любые электрохимические реакции, которые осуществляются в электрохимической системе при прохождении через неё n элект-ронов, получаем:

E = =

(6.2.8)

где индекс i относится к исходным веществам, участвующим в реакции n электронами, а индекс f - к продуктам этой реакции.

Если цепь полностью равновесна, то произведение активностей отдельных ионов в уравнении (6.2.8) всегда может быть заменено активностями нейтральных образований (солей, кислот) или же средними активностями. Так, например, для рассмотренной системы уравне-ние (6.2.7) можно переписать в виде

E = = (6.2.9)

Применим к электрохимическим цепям, находящимся при постоянном давлении, уравне-ние Гиббса-Гельмгольца¹

(6.2.10)

где – изменение энтальпии в ходе хими-ческой реакции.

Пусть химическая реакция является итогом электродных процессов в электрохимической цепи и соответствует прохождению через цепь n электронов. Разделив все члены уравнения (6.2.10) на nF и поменяв знаки, получаем с учётом формулы (6.2.6):

E = - + T . (6.2.11)

Так как 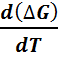= - то = Таким образом, температурный коэффициент ЭДС характери-зует изменение энтропии в ходе соответс-твующей химической реакции, а величина H характеризует общий тепловой эффект химической реакции при её обратимом протекании в условиях постоянного давления.

Будем рассматривать только произвольно протекающие химические реакции, для которых E . Электрохимические цепи такого вида называют гальваническими элементами.

Если 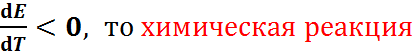, про-текающая в гальваническом элементе, может быть только экзотермической ( Поскольку при её протекании энтропия уменьшается (, то работа гальвани-ческого элемента должна сопровождаться выделением теплоты. Следовательно, в условиях теплоизоляции электрохимическая система будет нагреваться. Таким образом, при работе гальванического элемента в условиях 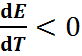за счет убыли энтальпии совершается работа nFE и выделяется теплота в количестве nFT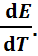

Если то реакция тоже может быть только экзотермической ( торабота гальванического элемента, со-вершаемая за счет убыли энтальпии, не должна сопровождаться тепловыми эффектами.

Если то протекающая в гальваничес-ком элементе химическая реакция сопровожда-ется ростом энтропии (. Поэтому при работе такого элемента происходит поглощение теплоты из окружающей среды. Если же электро-химическая цепь изолирована, то она охлажда-ется. При условии 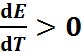, химическая реакция в элементе может быть как экзотермической, так и эндотермической. Если , то электри-ческая работа совершается за счет убыли энтальпии и поглощении тепла из окружающей среды. Если , то электрическая работа совершается только за счет роста энтропии в системе. Обычный путь использования химиче-ской энергии реакции в форме выделяющегося тепла здесь невозможен, так как тепловой эф-фект равен нулю. Наконец, если реакция эндоте-рмическая ( но Т , то, согласно уравнению (6.2.11), от гальванического элемента можно получить работу. В этих условиях за счет поглощения тепла в количестве, эквивалентном росту энтропии системы, не только совершается электрическая работа, но и увеличивается энта-льпия системы. Электрохимические цепи, отве-чающие таким необычным условиям, дейст-вительно можно реализовать. Примером может служить цепь

Ag, AgCl C , Hg | Ag,

в которой осуществляется реакция

C + Ag Hg + AgCl, (6.2.E)

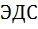этой цепи при 2 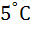Е = 0,0465 В, а 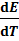= 3,39·1 В/град. Используя уравнение (6.2.11), находим измене-ние энтальпии:

=5,3·1 (Дж/моль) = 5,3 (кДж/моль).

Положительное значение указывает на эндотермический характер приведенной реакции. Аналогичным закономерностям подчиняются концентрационные цепи, для которых = 0 и которые работают за счёт возрастания энтропии системы.

Уравнения (6.2.6) и (6.2.11) можно исполь-зовать для нахождения термодинамических фун-кций, характеризующих химические реакции, которые протекают в гальваническом элементе. Так, ЭДС даёт изменение свободной энергии Гиббса, а стандартное значение ЭДС связано с константой равновесия химической реакции :

= ln 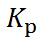. (6.2.12)

Величина характеризует полноту протекания химической реакции. Далее по температурному коэффициенту ЭДС можно рассчитать изменение энтропии в ходе химической реакции

(6.2.13)

А по совокупности данных E и - при помощи уравнения (6.2.11) определить измене-ние энтальпии и энтропии химической реакции на основе электрохимических измерений удоб-нее воспользоваться так называемой канониче-ской формой записи уравнения Гиббса-Гельм-гольца:

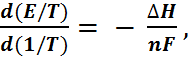(6.2.14)

которая, как нетрудно убедится, полностью эквивалентна уравнению (6.2.11). Как показы-вает опыт, зависимости 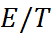от при пос-тоянном давлении в небольшом интервале температур оказываются практически линейны-ми. Согласно соотношению (6.2.14), их наклон равен / образом, в сочетании с уже известной величиной из об-щего соотношения второго начала термоди-намики G + T 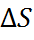можно рассчитать и изменение энтропии

Отметим, что уравнения (6.2.11), (6.2.12) и (6.2.14) применимы к так называемым «изоте-рмическим ячейкам», когда оба электрода галь-ванического элемента находятся при одинаковой температуре. Электрохимический метод широко применяется при исследовании термодинамиче-ских свойств различных химических процессов, на основе которых можно построить равнове-сные электрохимические цепи.

Электрохимические цепи строго равновесны лишь тогда, когда они не содержат ни одной границы двух различных растворов. На такой границе происходят неравновесные процессы диффузии и возникает диффузионный потенциал (см. главу 4). Тем не менее для многих химиче-ских реакций такой границы избежать не удаёт-ся. Так, например, при реализации в электро-химической системе реакции

Fe(II) + Ce(IV)

неизбежна граница между растворами, содер-жащими Fe(II) и Ce(IV) (см. Введение, рис. 1). Электрохимическая цепь, содержащая границу двух растворов, называется цепью с переносом. Схему цепи с переносом изображают следую-щим образом:

| раствор (I) раствор (II) ,

где пунктирная вертикальная черта указывает на существование между двумя растворами диффу-зионного потенциала. Диффузионный потенциал является гальвани –потенциалом между точками, находящимися в разных по химическому составу фазах, а потому его нельзя измерить. Если при-равнять изменение свободной энергии Гиббса, обусловленное переносом ионов через границу раздела двух растворов, электрической работе, то можно получить общую формулу для диффузи-онного потенциала:

= – , (6.2.15)

где – активность отдельного i- го иона; число переноса этого иона; зарядовое число иона с учётом знака

Для на границе двух бинарных элек-тролитов различной концентрации при единич-ных коэффициентах активности справедлива фо-рмула (4.2.22)

= . (4.2.22)

В общем случае, однако, активности отдельных ионов неизвестны, и точный расчет по формуле (6.2.15) невозможен. Если в разбав-ленных растворах активности отдельных ионов в первом приближении заменить их концентра-циями, то, задавшись определённым распреде-лением концентраций в области между двумя растворами, можно рассчитать с погреш-ностью, которая будет тем меньше, чем более разбавленные растворы находятся в контакте друг с другом. М. Планк впервые решил уравне-ние (6.2.15) в предположении о том, что подви-жности однозарядных ионов не зависят от конце-нтрации и что на границе двух растворов име-ется тонкий переходный слой, за пределами которого составы растворов остаются постоян-ными. При этом стационарное распределение концентрации ионов в неподвижном переходном слое устанавливаются самопроизвольно в соотве-тствии с законами диффузии и миграции. На опыте такие условия в первом приближении реализуются при контакте двух растворов через пористую диафрагму, по обе стороны от которой концентрации всех ионов поддерживаются постоянными за счет перемешивания растворов.

При выполнении этих условий для расчета М. Планк получил следующее трансцен-дентное уравнение:

(6.2.16)

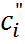
где ; предельная электро-проводность i –го иона; концентрация раствора I; концентрация раствора II.

В случае контакта двух растворов 1,1- вален-тных электролитов А и А с концентра-циями и 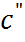cоответственно уравнение (6.2.16) можно привести к следующему более простому виду:

(k (6.2.17)

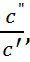
где x = k = и .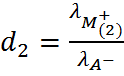

Интересно отметить, что уравнение (6.2.17), как, очевидно, и уравнение (6.2.16), имеет два решения. Одно из них, а именно x= однако, лишено физического смысла, так как даёт значение , которое не зависит от величин и и, таким образом, нечувст-вительно к различиям в подвижностях анионов и катионов.

Поскольку численное решение уравнения (6.2.16) является очень сложной процедурой, значительно большее распространение получила формула Гендерсона

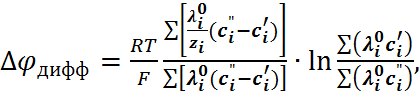(6.2.18)

которая выводится из общего уравнения (6.2.15) при замене активностей на концентрации и при допущении, что в относительно широком пере-ходном слое линейно изменяется от раствора I к раствору II, а концентрации выражены в г 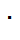экв/л. Для контакта двух растворов 1,1-валентных элек-тролитов с одинаковыми анионами, используя те же обозначения, что и в формуле (6.2.17), урав-нение (6.2.18) можно привести к виду

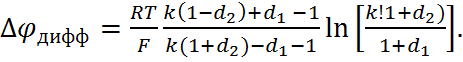(6.2.19)

Если указанные растворы имеют одинаковый состав и отличаются только концентрациями, то и оба уравнения (6.2.17) и (6.2.19) одно и то же выражение для диффузионного по-тенциала

(6.2.20)

которое совпадает с ранее полученной фор-мулой (4.2.22) при и Если же то уравнения Планка (6.2.17) и Гендерсон (6.2.19) приводят к различным значениям . Так, например, для границы 0,1 М НСl с 3,5 М раствором LiCl при температу-ре 20 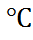, когда k = 35, и = 0,325, реше-ние уравнения (6.2.17) даёт = 47,4 мВ, а из формулы (6.2.19) получается = 35,7 мВ. Для проведения этого расчёта использованы значения и 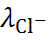, полученные экстраполя-цией, так как данные для 3,5 М раствора отсутствуют.

Разность потенциалов на концах электро-химической цепи с переносом содержит и, следовательно, отличается от ЭДС, которая используется для расчёта химической реак-ции. Введение поправок на диффузионный поте-нциал по формулам (6.2.16) (6.2.19), естест-венно приводит к ошибкам в При этом сле-дует учитывать, что ошибка в равная 1мВ, эквивалентна ошибке в , равной 0,1 кДж/моль. Существует способ резкого умень-шения диффузионного потенциала, который заключается в том, что между двумя растворами включают солевой мостик – концентрированный раствор соли, у которой 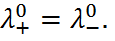Такими свойствами обладают, например, водные растворы KCl и . При включении солевого мостика одна граница между двумя растворами I и II заменяется двумя, например I и . Но на каждой из новых границ, в согласии с формулой (6.2.18), меньше, чем на первоначальной, и, кроме того, диф-фузионные потенциалы на новых границах обычно противоположны по знаку, так как общий их вклад в измеряемую разность резко снижается. Таким образом, измерение измеря-емой разности потенциалов при включении солевого мостика в первом приближении может служить мерой первоначального диффу-зионного потенциала¹.

__________________________

¹ В действительности 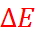равно алгебраичес-кой сумме трёх диффузионных потенциалов

,

но предполагается, что

Если величина хорошо согласуется со значением , рассчитанным по формуле(6.2.18), то диффузионный потенциал можно элиминировать и по исправленным значениям разности потенциалов проводить приближенные термодинамические расчёты. Так, например, на границе 0,1 М растворов HCl и NaCl = 33,1 мВ, а формула (6.2.18) даёт = 33,4 мВ. Электрохимическую цепь с переносом и элими-нированным диффузионным потенциалом схема-тически изображают следующим образом:

раствор (II)

где двойная пунктирная вертикальная черта ука-зывает на элиминирование (исключение, устра-нение) диффузионного потенциала между раст-ворами I и II.

Для электрохимических цепей с переносом уравнение Нернста (6.2.8) обычно не приводится к виду, содержащему средние активности ионов ². Поэтому при использовании уравнения Нернста для таких систем активности отдельных ионов заменяют средними активностями или просто концентрациями ионов. Вносимая при этом ошибка увеличивается с ростом концентрации.

__________________________

² Исключение составляют цепи, имеющие границу двух растворов одного итого же бина-рного электролита, но различной концентрации, если различие в концентрации этих двух раст-воров не очень значительно.

Не нашли, что искали? Воспользуйтесь поиском: