Закон Био-Савара-Лапласа

В соответствии с законом Био-Савара-Лапласа магнитная индукция поля, создаваемого элементом проводника с током 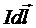в точке пространства, удаленной от этого элемента проводника на расстояние (рис. 4.3) равна:

, (4.4)

Формула (4.4) в скалярной форме:

,

где α – угол между векторам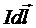и и . Направление вектора можно определить по правилу правого винта.

Закон Био-Савара-Лапласа позволяет найти индукцию магнитного поля в данной точке пространства от любой системы проводников с током. Для этого нужно воспользоваться принципом суперпозиции:

B = ∑ B_i или B = ∫ d B. (4.5)

Наиболее просто интеграл (4.5) вычисляется, если все векторы коллинеарные (индукция магнитного поля от прямолинейного проводника или на оси кругового проводника с током).

Определим магнитную индукцию на оси витка с током на расстоянии Х от центра контура (рис. 4.4).

Каждый элемент тока создает индукцию . Векторы перпендикулярны к плоскостям, проходящим через соответствующий элемент 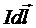и точку, в которой определяем поле. Следовательно, он и образует симметричный конический веер. Из соображений симметрии можно заключить, что результирующий вектор В направлен вдоль оси контура. Каждый из составляющих векторов вносит в результирующий вектора вклад , равный по модулю

, (4.6)

где R – радиус витка с током. Угол α между векторами и – прямой.

Поэтому результирующая индукция магнитного поля равна по модулю:

. (4.7)

Здесь использовано выражение . В центре кругового тока (х = 0) магнитная индукция равна

. (4.8)

Не нашли, что искали? Воспользуйтесь поиском: