Тема 1. Матрицы и определители. Системы линейных уравнений

1. Определитель после приведения к треугольному виду и применения теоремы Лапласа к первому столбцу может быть записан в виде …

Решение

Применим элементарные преобразования с целью приведения к треугольному виду:
.
Разложение по одной строке или столбцу есть частный случай теоремы Лапласа о разложении определителя по нескольким строкам или столбцам. Теперь разложим определитель в последней записи по первому столбцу: .

2. Дана матрица . Если – единичная матрица того же размера, что и матрица , то матрица равна …

Решение

Матрица С находится следующим образом:

.

3. Даны клеточные матрицы и .Размерность блоков – , – . Если произведение клеточных матриц и существует, то число строк в блоках 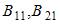равно…

Решение

При умножении блочных матриц можно оперировать с блоками как с отдельными элементами, не забывая, что каждый элемент также является матрицей. Ограничение на размерность правой матрицы-множителя при произведении матриц – совпадение числа строк с числом столбцов левой матрицы-множителя, ограничений на число столбцов правой матрицы нет. Поэтому исходя из размерностей и число строк равно 3, – 2.

4. Дана матрица , где 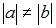. Тогда обратная матрица может быть представлена в виде …

Решение

Матрица называется обратной к квадратной матрице А, если , где Е – единичная матрица.
Обратная матрица может быть найдена по формуле , где 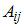– алгебраическое дополнение элемента матрицы и .
Находим: , , , , .
Следовательно, .

5. Если для системы уравнений

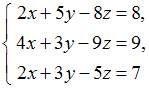
реализовать прямой ход метода Гаусса, то в итоге получится система уравнений …

Решение

Построим расширенную матрицу исходной системы уравнений

и все необходимые преобразования будем применять к этой и последующим матрицам.
К строке 2 прибавим строку 1, умноженную на (-2), а из строки 3 вычтем строку 1. Получим матрицу, эквивалентную исходной матрице
.
Строку 1 разделим на 2, а строку 2 разделим на (-7), тогда
.
К строке 3 прибавим строку 2, умноженную на 2, тогда
.
Прямой ход метода Гаусса завершён, матрица приведена к трапецеидальному виду. По последней матрице восстанавливаем систему уравнений (треугольного вида), равносильную исходной системе

Не нашли, что искали? Воспользуйтесь поиском: