Тема 2. Векторная алгебра. Аналитическая геометрия

1. Даны векторы . Тогда линейная комбинация этих векторов равна …

Решение

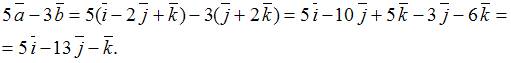
2. Точки и 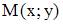лежат на одной прямой, параллельной оси абсцисс. Расстояние между точками А и М равно 5. Тогда отрицательные координаты точки М равны …

Решение

Для точек, лежащих на одной прямой, параллельной оси OX, выполняется условие: их ординаты равны. Следовательно, 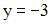и . Расстояние между двумя точкам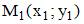и и находится по формуле:
. Тогда расстояние между точками А и M можно найти как: .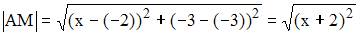
Из условия , получаем или .

3. С помощью преобразования параллельного переноса осей координат уравнение кривой приводится к каноническому виду…

Решение

Выделяя полные квадраты относительно переменных 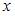и , получим: ;
;
.
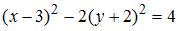Следовательно, . Тогда координаты центра кривой есть .
Выполним преобразование параллельного переноса системы координат в центр линии, то есть в точку , по формулам ; , где – новые координаты.
Тогда уравнение кривой в новой системе координат примет вид .
Это каноническое уравнение гиперболы.

4. Прямая 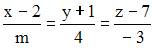и плоскость перпендикулярны при значениях m и С, равных …

Решение

Условие перпендикулярности прямой и плоскости имеет вид: 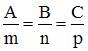или . Отсюда ; 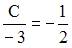или .

5. Уравнение является …

Решение

Уравнение можно представить в виде:
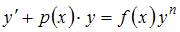, где . Действительно,
.
Поэтому оно является уравнением Бернулли.

Не нашли, что искали? Воспользуйтесь поиском: