Тема 3. Элементы математического анализа

1. Общее решение дифференциального уравнения при имеет вид …

Решение

Разделим переменные и проинтегрируем .
Тогда , где или , и общее решение примет вид , .

2. Общее решение дифференциального уравнения имеет вид …

Решение

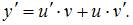Уравнение перепишем в виде Введем замену Тогда уравнение примет вид или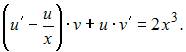
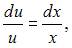Пусть Тогда и Подставив найденное значение u в уравнение 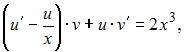получим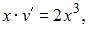 и Окончательное решение имеет вид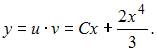

3. Решение задачи Коши 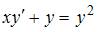, 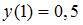имеет вид …

Решение

Уравнение можно привести к виду .
После разделения переменных получим , откуда 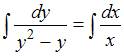. Так как , в левой части имеем .
Таким образом, общий интеграл уравнения имеет вид 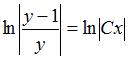, т.е. .
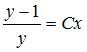Используя начальное условие 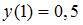, найдем . Таким образом, частный интеграл имеет вид . Из найденного частного интеграла, выполнив преобразования , , 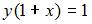получаем искомое частное решение .

4. Общее решение линейного однородного дифференциального уравнения второго порядка 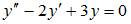имеет вид …

Решение

Составим характеристическое уравнение и решим его: . Тогда фундаментальная система решений примет вид
,
а общее решение примет вид
, где .

5. Общий вид частного решения линейного неоднородного дифференциального уравнения второго порядка будет выглядеть как …

Решение

Общее решение этого уравнения можно записать в виде где функция – общее решение однородного уравнения а функция – некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 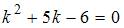и найдем его корни: 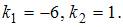Тогда общее решение однородного уравнения будет иметь вид
Поскольку правая часть исходного уравнения 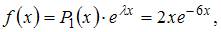то имеем уравнение со специальной правой частью.
Так как является корнем характеристического уравнения, то частное решение неоднородного уравнения будем искать в виде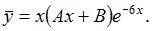

6. Общее решение системы дифференциальных уравнений

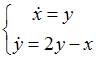
имеет вид …

Решение

Решим систему уравнений методом исключения.
Из первого уравнения имеем и, после подстановки выражений для и во второе уравнение системы, получим линейное дифференциальное уравнение 2-го порядка .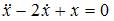
Характеристическое уравнение имеет один действительный корень кратности 2. Такому корню соответствует общее решение однородного дифференциального уравнения . Дифференцируя полученное решение, находим .
Тогда общее решение системы уравнений имеет вид .

Не нашли, что искали? Воспользуйтесь поиском: