Методические указания к решению типовых задач. Задача №7.1. Полная плотность тока в электролитах является суммой плотности тока положительных ионов и плотности тока отрицательных ионов:

Задача №7.1. Полная плотность тока в электролитах является суммой плотности тока положительных ионов и плотности тока отрицательных ионов: 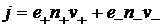. Почему масса вещества, выделившегося на катоде, пропорциональна полному току, а не току только положительных ионов?

Указания по решению. Действительно, масса выделившегося на катоде вещества равна массе всех ионов, пришедших к нему:

,

при этом ими будет перенесен заряд

.

С другой стороны, носителями тока в электролитах являются ионы обоих знаков. Увлекаемые электрическим полем ионы дрейфуют в противоположных направлениях (чаще всего с различной скоростью, одновременно участвуя в хаотическом тепловом движении). В средней части электролита через любое поперечное сечение в единицу времени проносится заряд, складывающийся из заряда прошедших через это сечение положительных и отрицательных ионов. Концентрации ионов каждого знака в условиях динамического равновесия между процессами ионизации и молизации можно считать постоянными и одинаковыми практически по всему объему электролита.

Однако вблизи электрода электрическое поле очищает раствор от ионов одного знака: вблизи катода почти отсутствуют отрицательные ионы, замыкают цепь на катоде лишь положительные ионы. Здесь ионы другого знака (по сравнению со знаком заряда электрода) вынуждены «спешить», чтобы самим осуществить весь электрический ток.

Поскольку каждый из ионов обязательно достигает своего электрода, то в конце концов его заряд нейтрализуется (фактически ион теряет лишние или приобретает недостающие электроны). Заряд уходит дальше по электрической цепи, а образовавшиеся незаряженные атомы выделяются (оседают) на электродах или вступают во вторичные химические реакции.

Задача №7.2. Металлическую поверхность с площадью S =200 см² надо покрыть слоем серебра толщиной d =20 мкм. Сколько минут надо пропускать ток силой I =0,5 А через электролит?

Указания по решению. Для покрытия указанной поверхности слоем серебра потребуется эту поверхность поместить в качестве катода в раствор соли серебра. В результате электролиза должно выделиться серебро объемом

,

масса которого, с учетом плотности серебра, равна

.

По первому закону Фарадея для электролиза запишем:

,

где суммарный прошедший через электролит заряд выразим на основе постоянства силы тока в течение всего времени серебрения:

.

Окончательно получаем:

,

откуда искомое время равно

,

где значения плотности и электрохимического эквивалента серебра даны в приложении 4.

Проверку размерности и вычисления произведите самостоятельно.

Задача №7.3. Какое количество электроэнергии W (в МДж) расходуется на получение m =1 кг алюминия, если электролиз ведется при напряжении U =9 В, а КПД установки h =50%?

Указания по решению. По определению коэффициента полезного действия

,

где А – полезная работа электрического тока по осуществлению электролиза, W – полная полученная установкой электроэнергия, включая потери и пр. Отсюда

.

В соответствии с формулой работы электрического тока

,

если сила тока не меняется, и

в общем случае. С другой стороны, по закону Фарадея для электролиза имеем

,

где k – электрохимический эквивалент алюминия (см. приложение 4). Выражаем из закона электролиза заряд и подставляем в формулу для работы:

,

откуда выражается искомая величина:

.

Вычисления произведите самостоятельно.

Задача №7.4. Определите электрохимический эквивалент натрия. Относительный атомный вес натрия считать известным.

Указания по решению. Воспользуемся вторым законом Фарадея для электролиза: электрохимический эквивалент k всякого вещества пропорционален его химическому эквиваленту Э, т.е.

,

где коэффициент пропорциональности является универсальной (для всех веществ одинаковой) постоянной, обратной постоянной Фарадея, т.е.

.

Химический эквивалент натрия есть отношение его атомного веса к его валентности (см. приложение 4).

Завершите решение задачи в общем виде, произведите расчет и сравните полученный результат с табличным значением искомой величины.

Задача №7.5. Воздух между пластинами плоского конденсатора ионизируется рентгеновским излучением. Сила тока, текущего между пластинами, I =10 мкА. Площадь каждой пластины конденсатора S =200 см², расстояние между ними d =1 см, разность потенциалов U =100 В. Подвижность положительных ионов b ₊=1,4 см²/(В×с) и отрицательных b _-=1,9 см²/(В×с), заряд каждого иона равен элементарному заряду. Определите концентрацию пар ионов между пластинами, если ток далек от насыщения. [9,5×10¹⁴ м^-3] (3, с.176)

Указания по решению. Т.к. по условию ток далек от насыщения, то в газе идет несамостоятельный разряд. При этом выполняется закон Ома в виде (7.5):

,

где n – концентрация ионов одного знака или, иначе говоря, концентрация пар ионов (положительный ион + электрон), т.е искомая величина. Выражаем ее:

.

Величину плотности тока найдем в соответствии с ее определением:

,

при этом предполагаем, что она постоянна, или, иначе, находим ее среднее значение. Величину напряженности поля получим на основе связи напряженности с разностью потенциалов:

- напряженность поля между пластинами плоского конденсатора.

Завершите самостоятельно решение задачи в общем виде и вычислите искомую концентрацию.

Задача №7.6. Ток насыщения при несамостоятельном разряде равен I_нас =9,6 пА. Определите число пар ионов, создаваемых в 1 с внешним ионизатором. [3×10⁷] (3, с. 176)

Указания по решению. В теории несамостоятельного газового разряда при наличии тока стационарное состояние газа характеризуется равенством:

,

где a – интенсивность ионизатора (число молекул, ионизируе­мых ежесекундно в единице объема газа), – число пар ионов, молизующихся за единицу времени в единице объема (В – коэффициент рекомбинации), – число пар ионов, уводи­мых под воздействием поля в единицу времени из единицы объема газа и нейтрализующихся на электродах, площадью S электродов с расстоянием d между ними.

В случае , т. е. когда плотность тока настолько велика, что вся убыль ионов практически будет определяться их нейтрализацией на электродах, условие равновесия принимает вид

.

Обозначив плотность тока, удовлетворяющую этому равенству, через , получим

.

Отсюда следует, что величина (плотность тока насыще­ния) не зависит от напряженности поля, а следовательно, и от напряжения между электродами: при этом все ионы, производимые ионизатором, уводятся то­ком из газа и целиком нейтрализуются на электродах.

Получаем

,

где произведение есть искомая величина.

Задача №7.7. Опираясь на МКТ газов, сравните длину свободного пробега электрона при несамостоятельном газовом разряде с длиной свободного пробега нейтральной молекулы.

Указания по решению. Средняя длина свободного пробега газовых молекул опреде­ляется известной формулой молекулярной физики:

, (1)

где n – число молекул в единице объема, d – эффективный диа­метр молекул, равный сумме эффективных радиусов r ₁и r ₂стал­кивающихся молекул:

.

Заметим, что взнаменателе приведенной формулы является следствием учета движения соударяемых молекул.

Движение электронов в газовой среде подобно движению га­зовых молекул. Длина свободного пробега электрона, характеризующая средний путь между двумя последовательными столкновениями с молекулами газа может быть определена по этой же формуле с учетом 2-х обстоятельств:

1) радиус электрона намного меньше радиуса молекулы, по­этому в выражении для эффективного диаметра ра­диусом электрона r ₂ можно пренебречь по сравнению с радиу­сом молекулы r ₁: ;

2) ско­рость электрона, благодаря его незначительной массе, гораздо больше скорости молекул, поэтому нет необходимости сохранять в знаменателе формулы.

Таким образом, средняя длина свободного пробега электронов в газовой среде равна

, (2)

где r – эффективный радиус молекул газа.

Так как в формуле d =2 r, то из (1) и (2) следует, что

,

т.е. средняя длина свободного пробега электронов приблизительно в 5,6 раза больше соответствующей величины для молекул газа.

Не нашли, что искали? Воспользуйтесь поиском: