
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методические указания к решению типовых задач. Задача №6.1. Дана цепь, изображенная на рис
 Задача №6.1. Дана цепь, изображенная на рис. 31. Определите силу тока в каждом элементе и напряжение на зажимах реостата, если E1=12 В, r 1=1 Ом, E2=6 В, r 2=1,5 Ом и R =20 Ом. Каковы параметры источника тока, эквивалентного двум данным, соединенным параллельно?
Задача №6.1. Дана цепь, изображенная на рис. 31. Определите силу тока в каждом элементе и напряжение на зажимах реостата, если E1=12 В, r 1=1 Ом, E2=6 В, r 2=1,5 Ом и R =20 Ом. Каковы параметры источника тока, эквивалентного двум данным, соединенным параллельно?
|
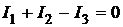 .
.
Т.к. число ветвей в данной цепи р =3, то независимых контуров в схеме будет  : АСDB и ABNM, они являются элементарными контурами цепи. В направлении указания обозначений, т.е. по часовой стрелке, выберем и положительное направление обхода каждого из них. Записываем еще 2 уравнения на основе (6.2) для указанных контуров соответственно:
: АСDB и ABNM, они являются элементарными контурами цепи. В направлении указания обозначений, т.е. по часовой стрелке, выберем и положительное направление обхода каждого из них. Записываем еще 2 уравнения на основе (6.2) для указанных контуров соответственно:

Получаем систему из трех уравнений для искомых сил токов в ветвях, которая, после подстановки числовых данных из условия задачи, принимает вид:

Находим решение этой системы в Mathcad:
I 1=2,68 А,
I 2=-2,214 А,
I 3=0,466 А.
Отсюда ясно, что истинное направление тока через второй элемент противоположно указанному на рис. 31.
Падение напряжения на зажимах реостата
 (В).
(В).
Найдем на основе правил Кирхгофа и закона Ома для полной цепи формулы, определяющие параметры источника, эквивалентного двум параллельно соединенным элементам с ЭДС E1 и E2 и внутренними сопротивлениями r 1 и r 2 (см. табл. 3).
Самостоятельно рассчитайте по данным задачи параметры эквивалентного источника, по закону Ома для полной цепи найдите ток I через сопротивление и сравните его с ранее полученным значением I 3.
Таблица 3
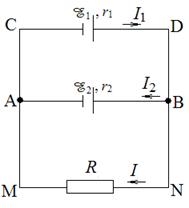  отсюда
отсюда  , подставляем во второе уравнение: , подставляем во второе уравнение:
 Далее из 2-го уравнения последней системы выражаем
Далее из 2-го уравнения последней системы выражаем
 и подставляем в первое уравнение:
и подставляем в первое уравнение:
 Умножим обе части последнего равенства на величину
Умножим обе части последнего равенства на величину  и упростим правую часть, получим и упростим правую часть, получим
 или
или

| 

|
Сравнивая последние формулы каждой колонки, видно:
 и
и
 что и отражает факт параллельного соединения сопротивлений r 1 и r 2.
что и отражает факт параллельного соединения сопротивлений r 1 и r 2.
|
|
 Задача №6.2. При решении задач с несколькими источниками ЭДС можно сначала рассчитать токи, создаваемые каждым источником ЭДС, потом найти полный ток, как сумму этих токов. Этот способ вполне законен, если при расчетах принимать во внимание внутреннее сопротивление источников, и называется методом суперпозиции (наложения). Определите, используя этот метод, ток между узлами А и В. Даны сопротивления R 1=4 Ом, R 2=3 Ом, R 3=12 Ом и напряжения на клеммах источников U 1=40 В, U 2=72 В (рис. 32). [8 А] (6, с. 241)
Задача №6.2. При решении задач с несколькими источниками ЭДС можно сначала рассчитать токи, создаваемые каждым источником ЭДС, потом найти полный ток, как сумму этих токов. Этот способ вполне законен, если при расчетах принимать во внимание внутреннее сопротивление источников, и называется методом суперпозиции (наложения). Определите, используя этот метод, ток между узлами А и В. Даны сопротивления R 1=4 Ом, R 2=3 Ом, R 3=12 Ом и напряжения на клеммах источников U 1=40 В, U 2=72 В (рис. 32). [8 А] (6, с. 241)Указания по решению. Из закона Ома для полной цепи следует, что напряжение на клеммах источника меньше его ЭДС на величину падения напряжения на его внутреннем сопротивлении:

Поэтому, оперируя напряжениями, не надо рассматривать внутренние сопротивления соответствующих источников напряжения.
Расчет сложных цепей по методу наложения целесообразно применять в том случае, если, приравнивая нулю все ЭДС, кроме одной, упрощают цепь (получая, например, параллельно-последовательные цепи). При этом последовательность действий следующая:
1. Предположить, что в цепи существует только один источник ЭДС, например E1, а остальные источники ЭДС заменить резисторами с сопротивлениями, равными их внутренним сопротивлениям. В случае, если заданы не ЭДС, а напряжения на клеммах источников, остальные источники просто не учитываются.
2. Упростив полученную схему с одним источником ЭДС с учетом законов параллельного и последовательного соединений сопротивлений, вычислить токи Ij ¢ в каждой ветви (здесь индекс j принимает значения от 1 до р, где р – число ветвей в исходной цепи). Направление токов Ij ¢ определяется с учетом направления оставленного (единственного) источника ЭДС.
3. Проделать пункты 1 и 2 с каждым из других источников тока: E2, E3 и т.д. Получить значения и направления токов Ij ¢¢, Ij ¢¢¢ и т.д.
4. Вычислить истинные токи в ветвях по правилу: ток каждой ветви цепи Ij равен алгебраической сумме токов, протекающих под действием каждой ЭДС в отдельности. Правило знаков: слагаемые токи, протекающие в ветви в противоположных направлениях, берутся с противоположными знаками. Направление истинного тока совпадает с направлением, в котором сумма протекающих токов от отдельных ЭДС больше.
Переходим к решению задачи.
1) Оставляем в цепи первый источник и получаем схему на рис. 33, а). Здесь сопротивления R 2 и R 3 соединены параллельно:

или по закону Ома
 ,
,
 |
их общее сопротивление
 (Ом).
(Ом).
|
 (Ом).
(Ом).
Находим ток I 1¢:
 (А).
(А).
Зная этот ток, найдем два другие из системы уравнений:
 .
.
Получаем:
 ,
,
 (А),
(А),
тогда  (А).
(А).
 1) Оставляем в цепи второй источник напряжения и получаем схему на рис. 34. Здесь сопротивления R 1 и R 2 соединены параллельно:
1) Оставляем в цепи второй источник напряжения и получаем схему на рис. 34. Здесь сопротивления R 1 и R 2 соединены параллельно:

или по закону Ома
 ,
,
|
 (Ом).
(Ом).
Сопротивления R 12 и R 3 соединены последовательно, поэтому полное внешнее сопротивление, подключенное к источнику напряжения U 2, равно
 (Ом).
(Ом).
Находим ток I 3¢¢:
 (А).
(А).
Зная этот ток, найдем два других из системы уравнений:
 .
.
Получаем:
 ,
,
 (А),
(А),
тогда  (А).
(А).
Искомый ток во 2-й ветви равен алгебраической сумме токов I 2¢ и I 2¢¢. Эти токи направлены одинаково, поэтому
 =5+3=8 (А).
=5+3=8 (А).
 Задача №6.3. Элементы схемы, изображенной на рис. 35, имеют следующие значения: E1=1 В, E2=2 В, E3=3 В, R 1=100 Ом, R 2=200 Ом, R 3=300 Ом, R 4=400 Ом. Определите токи I 1 – I 4, текущие через сопротивления. Сопротивлением источников и соединительных проводов пренебречь. [4,545 мА; 7,273 мА; 11,818 мА; 0] (7, с. 137)
Задача №6.3. Элементы схемы, изображенной на рис. 35, имеют следующие значения: E1=1 В, E2=2 В, E3=3 В, R 1=100 Ом, R 2=200 Ом, R 3=300 Ом, R 4=400 Ом. Определите токи I 1 – I 4, текущие через сопротивления. Сопротивлением источников и соединительных проводов пренебречь. [4,545 мА; 7,273 мА; 11,818 мА; 0] (7, с. 137)
|
1. Выбрать и обозначить на схеме элементарные контуры.
2. Каждому элементарному контуру приписать произвольно направленный контурный ток. Удобно всем контурным токам задать одно и тоже направление[10] (например, по часовой стрелке), совпадающее с направлением обхода контуров. Число различных контурных токов равно числу независимых (в частности, элементарных) контуров, т.е. (р – n + 1).
3. Направления токов в ветвях можно указать произвольно, но токи во внешних ветвях будем изображать сонаправленными с выбранным направлением соответствующих контурных токов (например, по часовой стрелке).
4. Записать (р – n + 1) уравнений по второму правилу Кирхгофа с учетом внутренних сопротивлений источников ЭДС (падения напряжений на внутренних сопротивлениях источников складываются с падениями напряжений на других сопротивлениях контуров). При этом учитываем: 1) контурные токи, проходящие по внешним ветвям, являются для этих ветвей реально существующими; 2) контурные токи внутренних контуров являются фиктивными величинами, введенными для удобства расчетов; реальные токи внутренних ветвей равны разности[11] 2-х контурных токов контуров, которым эта ветвь принадлежит.
5. Решив систему, найти все контурные токи (некоторые значения могут быть отрицательными).
6. Найти действительные токи ветвей: 1) ток внешней ветви совпадает с соответствующим положительным контурным токов и противоположен отрицательному; 2) ток внутренней ветви, определяемый как разность контурных токов, совпадает с «истинным[12]» направлением большего (по модулю) контурного тока.
7. На основе полученных результатов изобразить на новой схеме истинные направления токов во всех ветвях.
8. Преимущество этого метода: вместо системы из р уравнений по первому и второму правилам Кирхгофа решается система из (р – n + 1) уравнений только по второму правилу Кирхгофа.
Переходим к решению задачи.
На данной схеме есть 3 элементарных контура: ABCL, LCDM и MNKA. Для них задаем контурные токи Iа, Ib, Iс. Указываем на схеме направления контурных токов, считая их одновременно и направлениями обхода соответствующих контуров. Внешних ветвей 3: ABC, CDM, NK, токи в них численно равны контурным токам Iа, Ib, Iс соответственно. Внутренние ветви: AL, LM и MLA, токи в них выражаются так:

 ,
,
 .
.
 .
.
Однако при записи уравнений необходимо все время учитывать правило знаков для второго закона Кирхгофа.
|
Имеем р =6 – число ветвей, n =4 – число узлов, получим (р – n + 1)=3 уравнения с 3-мя неизвестными Iа, Ib, Iс:

Раскроем скобки и подставим числовые данные:

Получим решение этой системы в Mathcad:
Iа =4,545 (мА),
Ib = – 7,273 (мА),
Iс =0 (мА).
Находим токи в ветвях:
 (мА), направлен как Iа.
(мА), направлен как Iа.
 (мА), направлен противоположно Ib.
(мА), направлен противоположно Ib.
 (мА), направлен противоположно Ib.
(мА), направлен противоположно Ib.
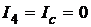 (мА),
(мА),
 (мА), направлен как Iа.
(мА), направлен как Iа.
 (мА), направлен противоположно Ib, т.к. этот контурный ток получился отрицательным (рис. 37).
(мА), направлен противоположно Ib, т.к. этот контурный ток получился отрицательным (рис. 37).
|

Сделайте проверку полученных значений на основе 2-х правил Кирхгофа.
Не нашли, что искали? Воспользуйтесь поиском: