
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методические указания к решению типовых задач. Задача №5.1. В проводе длины l полный движущийся заряд, равномерно распределенный по проводу, равен q
Задача №5.1. В проводе длины l полный движущийся заряд, равномерно распределенный по проводу, равен q. Определите среднюю скорость  движения зарядов, если ток равен I. [
движения зарядов, если ток равен I. [  ] (6, с. 227)
] (6, с. 227)
Указания по решению. Из условия задачи следует, что сила тока в проводе постоянна. Это значит, что при движении заряженных частиц, создающих ток, полный движущийся заряд в объеме провода не меняется.
Рассмотрим время D t, за которое отдельная частица – носитель тока – переместится с одного конца провода на другой, пройдя путь l (равный длине провода) со средней скоростью движения  :
:
 .
.
При этом через произвольное поперечное сечение проводника (расположенное в любом месте провода) будет перенесен заряд q. По определению силы тока
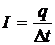 ,
,
т.к. ток постоянен.
Исключая из полученных равенств время D t, легко получить ответ к задаче в общем виде.
Подумайте, в каком месте решения задачи было учтено равномерное распределение зарядов по объему провода?
Задача №5.2. Из материала с удельным сопротивлением 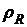 изготовлено плоское кольцо толщины d. Радиусы кольца равны а и b (b > a). Между внешней и внутренней цилиндрическими поверхностями кольца поддерживается некоторая разность потенциалов. Найдите сопротивление R кольца в этих условиях. [
изготовлено плоское кольцо толщины d. Радиусы кольца равны а и b (b > a). Между внешней и внутренней цилиндрическими поверхностями кольца поддерживается некоторая разность потенциалов. Найдите сопротивление R кольца в этих условиях. [ 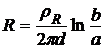 ] (7, с. 132)
] (7, с. 132)
Указания по решению. Формула сопротивления линейного проводника
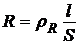 ,
,
|
 где
где 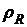 - удельное сопротивление материала проводника, l – его длина, S – площадь поперечного сечения, подразумевает, что напряжение будет подаваться на концы этого проводника (при этом длина становится расстоянием, которое проходят носители тока между точками, с заданной разностью потенциалов).
- удельное сопротивление материала проводника, l – его длина, S – площадь поперечного сечения, подразумевает, что напряжение будет подаваться на концы этого проводника (при этом длина становится расстоянием, которое проходят носители тока между точками, с заданной разностью потенциалов).
В данной задаче эта формула применима в виде
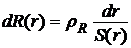
лишь для элемента кольца высотой, равной d, (рис. 19), где r – радиус этого элемента, dr – его толщина в радиальном направлении. Выражаем

и суммируем по всем элементам, т.е. при 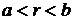 . Искомая величина получается интегрированием:
. Искомая величина получается интегрированием:
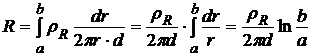 .
.
Самостоятельно, получите выражение для сопротивления этого же кольца в случае, когда напряжение подается на его верхнее и нижнее кольцевые поверхности. Произведите расчет, задавшись конкретными значениями величин, и сравните полученные результаты.
|
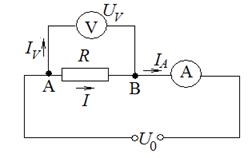 Задача №5.3. Резистор и амперметр соединены последовательно и подключены к источнику тока. К концам резистора присоединен вольтметр с сопротивлением
Задача №5.3. Резистор и амперметр соединены последовательно и подключены к источнику тока. К концам резистора присоединен вольтметр с сопротивлением 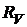 =4 кОм. Амперметр показывает силу тока IА =0,3 А, вольтметр – напряжение UV =120 В. Определите сопротивление резистора[7]. (6, с. 238)
=4 кОм. Амперметр показывает силу тока IА =0,3 А, вольтметр – напряжение UV =120 В. Определите сопротивление резистора[7]. (6, с. 238)Указания по решению. В условии описана разветвленная цепь (точки разветвления на схеме помечены черными кружками). Заметим (см. рис. 20), что ток, идущий через амперметр, не равен току, текущему через резистор!
Важно подчеркнуть, что амперметр показывает величину тока, текущего через этот амперметр, а вольтметр показывает напряжение на «своих» зажимах.
|
 При этом т.к. резистор и вольтметр соединены параллельно, то по закону параллельного соединения напряжения на всех параллельных сопротивлениях одинаковы (без учета сопротивлений соединительных проводов, которые пренебрежимо малы). А поэтому показание вольтметра UV в данном случае совпадает со значением напряжения и на сопротивлении R, и на всем участке между точками А и В с общим сопротивлением, равным
При этом т.к. резистор и вольтметр соединены параллельно, то по закону параллельного соединения напряжения на всех параллельных сопротивлениях одинаковы (без учета сопротивлений соединительных проводов, которые пренебрежимо малы). А поэтому показание вольтметра UV в данном случае совпадает со значением напряжения и на сопротивлении R, и на всем участке между точками А и В с общим сопротивлением, равным
 .
.
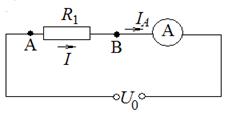
Рассмотрим новую неразветвленную схему (рис. 21), которая будет эквивалентна данной. Из этой схемы ясно видно, что через сопротивление R 1 и амперметр течет один и тот же ток, равный IА.
Запишем закон Ома для однородного участка цепи АВ:
 .
.
Подставив сюда выражение для R 1, получим равенство для нахождения искомой величины.
Завершите решение задачи самостоятельно. Дополнительно можно рассчитать токи, текущие через резистор I и вольтметр IV и определить разницу между показанием амперметра и величиной тока, текущего через резистор:
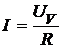 ,
,
 .
.
Проведите расчеты самостоятельно и сравните величины IV и (IА – I).
 Задача №5.4. Сечение медного провода длиной l =100 м меняется по закону S = S 0×(1+ kx), где S 0=1 мм2, k =0,01 м-1. По проводу течет ток I = 0,02 А. Определите силу, действующую на отдельные свободные электроны со стороны электрического поля.
Задача №5.4. Сечение медного провода длиной l =100 м меняется по закону S = S 0×(1+ kx), где S 0=1 мм2, k =0,01 м-1. По проводу течет ток I = 0,02 А. Определите силу, действующую на отдельные свободные электроны со стороны электрического поля.
Указания по решению. В задаче №5.2 рассматривалась формула сопротивления линейного проводника
|
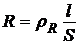 , (1)
, (1)
где 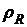 - удельное сопротивление материала проводника, l – его длина, S - площадь поперечного сечения, которая применима в случае однородного (
- удельное сопротивление материала проводника, l – его длина, S - площадь поперечного сечения, которая применима в случае однородного (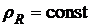 ) проводника постоянного поперечного сечения.
) проводника постоянного поперечного сечения.
В данной задаче сечение меняется по известному закону, поэтому записанная выше формула может быть использована лишь применительно к малому участку провода (с длиной участка dx), в пределах которого сечение можно считать постоянным. Решение задачи, таким образом, сводится к следующему:
1) разбиваем провод на малые участки постоянного сечения S (x);
2) по формуле (1) находим для каждого участка его сопротивление, т.е.
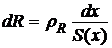 ;
;
3) т.к. полученные участки провода соединены между собой последовательно, то их общее сопротивление (сопротивление всего провода) по закону последовательного соединения равно сумме (интегралу) найденных сопротивлений всех участков:
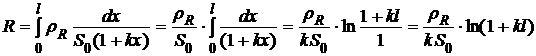 .
.
Значение удельного сопротивления меди находится по справочной таблице приложения 4.
Далее запишем закон Ома для участка «провод»[8]:
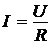 ,
,
где U – напряжение на концах провода, которое с учетом найденного выше сопротивления провода в дальнейшем считаем известным.
Вспомним связь разности потенциалов (напряжения) между двумя точками электрического поля и величиной напряженности, которая в случае однородного электрического поля записывается в простом виде:
 ,
,
где l – расстояние вдоль силовой линии поля между точками, к которым приложено напряжение U. В данном случае это – длина провода. Отсюда можно найти величину напряженности электрического поля в проводе, которое действует на отдельные носители тока в нем – свободные электроны – с силой
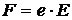 .
.
Самостоятельно получите общее решение задачи, сделайте проверку размерности и проведите вычисления.
Задача №5.5. Даны N =12 элементов с ЭДС E =1,5 В и внутренним сопротивлением r =0,4 Ом. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R =0,3 Ом; 1 Ом; 3 Ом? Определите максимальную силу тока.
Указания по решению. Обозначим n – число элементов, которые соединяются параллельно, тогда (N – n) элементов будут подсоединены к ним последовательно. Запишем, чему будут равны ЭДС и внутреннее сопротивление полученного соединения элементов:
Eбатареи=E+(N – n)E=(N – n + 1)E,
т.к. параллельное соединение одинаковых ЭДС (одноименными полюсами!) не меняет ее значения, а при последовательном соединении (разноименными полюсами) ЭДС частей суммируются, и
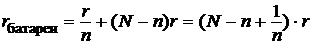 ,
,
т.к. параллельное соединение n одинаковых сопротивлений уменьшает их общее сопротивление в n раз, а сопротивления последовательных участков складываются.
|
 Собранная таким образом батарея включается в цепь с сопротивлением R (рис. 23), записываем закон Ома для этой цепи:
Собранная таким образом батарея включается в цепь с сопротивлением R (рис. 23), записываем закон Ома для этой цепи:

Произведем расчеты значений силы тока в системе Mathcad для разных значений n от 1 до 12 и для различных значений внешней нагрузки и результаты занесем в таблицу:
| Число параллельно соединенных элементов из 12-ти n | R =0,3 Ом | R =1 Ом | R =3 Ом |
| Сила тока I, А | |||
| 3,53 | 3,10 | 2,31 - наибольшее | |
| 3,67 | 3,173 - наибольшее | 2,29 | |
| 3,72 | 3,169 | 2,23 | |
| 3,75 | 3,14 | 2,14 | |
| 3,77 | 3,09 | 2,04 | |
| 3,80 | 3,03 | 1,92 | |
| 3,82 | 2,94 | 1,78 | |
| 3,85 | 2,83 | 1,61 | |
| 3,89 | 2,67 | 1,41 | |
| 3,95 | 2,45 | 1,17 | |
| 4,07 | 2,09 | 0,87 | |
| 4,5 - наибольшее | 1,45 | 0,45 |
Проанализируйте полученные значения и сделайте вывод.
Задача №5.6. Определите напряженность электрического поля в алюминиевом проводнике объемом V =10 см3, если при прохождении по нему постоянного тока в течение t =5 мин выделилось Q =2,3 Дж теплоты.
Указания по решению. Количество теплоты Q, выделившейся в алюминиевом проводнике сопротивлением R при прохождении по нему постоянного тока I в течение времени t, находится по закону Джоуля-Ленца в интегральной форме:
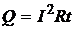 .
.
Из условия задачи не ясно, какова форма проводника, поэтому будем считать его линейным и его сопротивление считаем равным
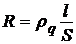 ,
,
где 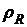 - удельное сопротивление алюминия (табличная величина), l – его длина, S - площадь поперечного сечения, которую считаем постоянной.
- удельное сопротивление алюминия (табличная величина), l – его длина, S - площадь поперечного сечения, которую считаем постоянной.
Искомую напряженность электрического поля в проводнике выразим по аналогии с задачей 5.4:
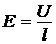 .
.
Осталось записать связь между током, напряжением на концах проводника и его сопротивлением в соответствии с законом Ома для однородного участка «данный алюминиевый проводник»:
 .
.
Мы рассмотрели 4 основные взаимосвязи между величинами, прямо или косвенно затронутыми в условии задачи. Попытаемся, исходя из этого, найти искомую величину. Для этого подставим в первое равенство последующие три:
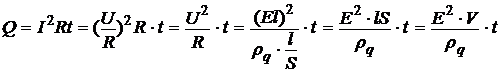 ,
,
отсюда и получается решение задачи в общем виде.
Завершите самостоятельно решение задачи, сделайте проверку размерностей и получите числовой результат.
Задача №5.7. Сила тока в проводнике сопротивлением R =10 Ом за время D t =50 с равномерно возрастает от I 1=5 А до I 2=10 А. Определите: 1) заряд, протекший через поперечное сечение проводника за указанное время; 2) количество теплоты, выделившееся за это время в проводнике.
 Указания по решению. При решении этой задачи будем использовать 2 метода: графический и так называемый «метод среднего», а также аналогию с кинематикой материальной точки.
Указания по решению. При решении этой задачи будем использовать 2 метода: графический и так называемый «метод среднего», а также аналогию с кинематикой материальной точки.
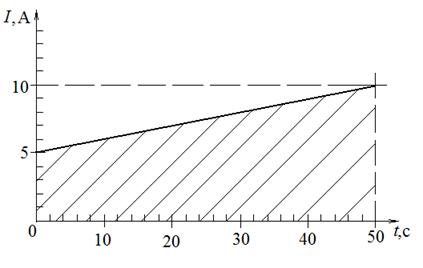
Построим график изменения со временем силы тока в проводнике (рис. 24).
|
I способ (графический). Известно из кинематики, что при неравномерном прямолинейном движении тела (когда скорость меняется по величине) в течение некоторого промежутка времени пройденный за это время путь графически представляется площадью криволинейной трапеции под графиком зависимости v (t) в соответствующем рассматриваемому отрезку движения временном интервале. Аналогично (с учетом таблицы 2 на стр. 70) искомый заряд равен площади заштрихованной фигуры на рис. 24, т.е. q =375 Кл.
II способ («метод среднего»). Из кинематики известно, что в случае равномерного возрастания скорости (равноускоренное движение) средняя на участке скорость равна среднему арифметическому от значений скорости в начале и в конце рассматриваемого участка движения. По аналогии найдем в данном случае среднее значение силы тока:
 (А).
(А).
Тогда также, как, зная среднюю скорость, находится весь пройденный путь, суммарный прошедший через поперечное сечение заряд будет равен
 (Кл).
(Кл).
Легко видеть, что полученные разными способами результаты совпадают.
2) Будем теперь искать количество теплоты, выделившееся за это время в проводнике.
Прежде всего, найдем искомое значение в соответствии с законом Джоуля-Ленца:
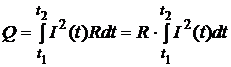 , (*)
, (*)
где, согласно таблице 2, сила тока меняется по закону
 .
.
Подставляем и вычисляем
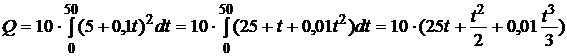 =29,17 (кДж).
=29,17 (кДж).
Возникает вопрос №1: можно ли как-то применить графический метод для нахождения теплоты?
Ответ: можно, но нужно будет (в соответствии с формулой (*)) искать площадь под графиком функции 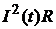 , который в данном случае представляет собой кусок параболы. Ясно, что по такому графику не удастся достаточно точно определить искомую величину.
, который в данном случае представляет собой кусок параболы. Ясно, что по такому графику не удастся достаточно точно определить искомую величину.
Далее возникает вопрос №2: нельзя ли тогда при решении использовать «метод среднего»?
Ответ: можно, но для этого необходимо знать «процедуру усреднения», отличную от той, что применялась при решении первой части задачи.
Действительно, любое усреднение нацелено на «совпадение результатов». Если в случае переменной величины (подлежащей в дальнейшем усреднению) результат имеет значение Y, то после проведения процедуры усреднения дальнейшее целесообразное использование полученного среднего значения должно давать тот же результат Y. В примере из кинематики это – «тот же путь за то же время». В первой части решения задачи это по аналогии есть – «тот же заряд за то же время»!
Поэтому при нахождении теплоты требуется прежде решить вопрос о том, как необходимо провести усреднение по иному результату: «то же количество теплоты за то же время». Но это уже вопрос дополнительных исследований, выходящий за рамки данного издания. Похожая процедура определена для случая синусоидального переменного тока: вспомните определение действующего значения переменного тока.
Задача №5.8. Проводка от магистрали к зданию имеет сопротивление 2 R =0,5 Ом. Напряжение в магистрали постоянно и равно U 0=127 В. Какова максимально допустимая потребляемая в здании мощность Р, если напряжение на включенных в сеть приборах не должно падать ниже U min=120 В?
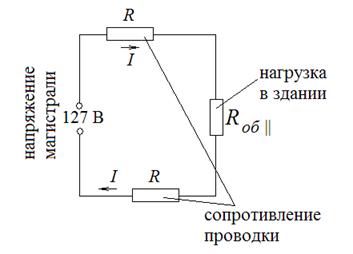
Указания по решению. Представим описанную в условии задачи цепь на схеме (рис. 25).
Заметим, что все приборы в здании подключаются параллельно, т.е. напряжение на них одинаково. Потребляемая каждым прибором мощность зависит от его сопротивления и с учетом закона Ома равна:
 ,
,
где U – напряжение, подведенное к зданию, которое по условию не должно падать ниже U min.
Потребляемая в здании мощность Р равна сумме мощностей, потребляемых всеми подключенными к сети приборами:
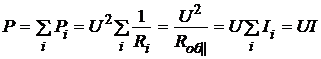 ,
,
где  – общее сопротивление параллельно соединенных приборов, I – ток идущий по проводке.
– общее сопротивление параллельно соединенных приборов, I – ток идущий по проводке.
 При увеличении числа приборов, включенных в сеть в здании, увеличивается их общее сопротивление
При увеличении числа приборов, включенных в сеть в здании, увеличивается их общее сопротивление  . При этом меняется ток во всей цепи по закону Ома для участка цепи «подводка + нагрузка в здании»:
. При этом меняется ток во всей цепи по закону Ома для участка цепи «подводка + нагрузка в здании»:
|
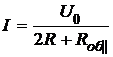
и напряжение на включенных в сеть приборах:
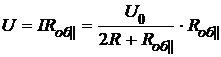 .
.
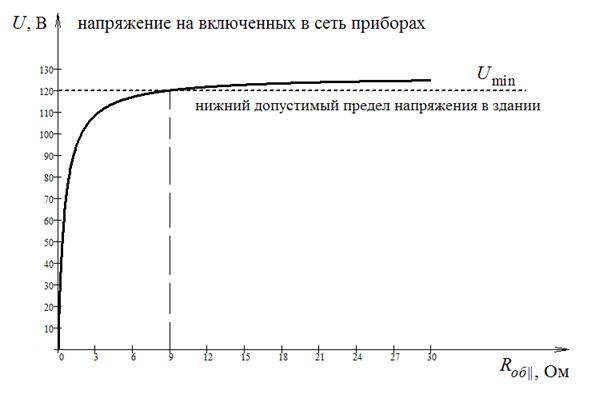
Построим с помощью системы Mathcad график зависимости напряжения в сети от сопротивления нагрузки  по данным из условия задачи (рис. 26).
по данным из условия задачи (рис. 26).
Подставляем в формулу для суммарной потребляемой мощности выражение для тока и получаем:
 .
.
Графически эта зависимость представлена на рис. 27.
|
|
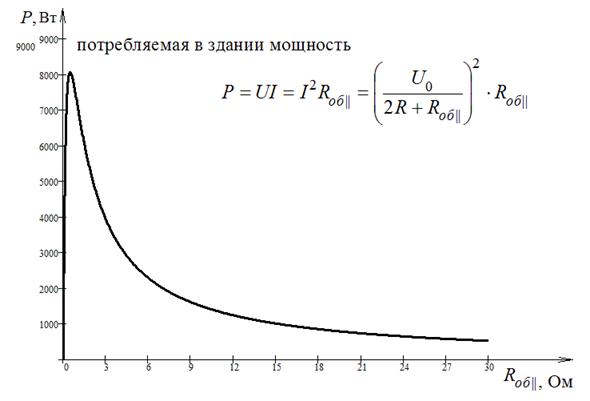
Сопоставляя оба графика, видно, что в области допустимых напряжений (U > U min) наибольшая потребляемая мощность соответствует наименьшему напряжению в сети. Т.е. искомая мощность соответствует значению U min:
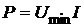 ,
,
где силу тока найдем из закона Ома для участка цепи «подводка»:
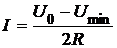 .
.
Окончательно имеем:
 .
.
Вычислим:
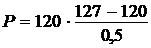 =1680 (Вт) = 1,68 (кВт).
=1680 (Вт) = 1,68 (кВт).
Задача №5.9. Обкладкам конденсатора емкости С =2 мкФ сообщаются разноименные заряды q 0=1 мКл. Затем обкладки замыкаются через сопротивление R =5000 Ом. Найдите: 1) закон изменения тока, текущего через сопротивление; 2) заряд q, прошедший через сопротивление за время t =2 мс; 3) количество теплоты Q, выделившееся в сопротивлении за то же время. [1) 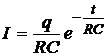 ; 2)
; 2) 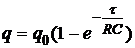 =0,18 мКл; 3)
=0,18 мКл; 3) 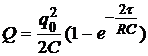 =82 мДж] (7, с. 133)
=82 мДж] (7, с. 133)
Указания по решению. 1) Закон изменения тока есть зависимость величины силы тока от времени. Начало отсчета времени в данном случае совпадает с моментом замыкания конденсатора через сопротивление и соответствует тому, что при t =0: 1) заряд на обкладках конденсатора равен q 0, 2) напряжение на сопротивлении равно напряжению на конденсаторе  , 3) сила тока по закону Ома для участка «сопротивление»
, 3) сила тока по закону Ома для участка «сопротивление» 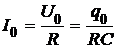 .
.
Ясно, что указанные соотношения между начальными значениями заряда, напряжения и тока выполняются в любой другой момент времени. Прежде всего, происходит разряд конденсатора, уменьшение заряда на его обкладках, т.е. имеет место какая-то зависимость заряда конденсатора от времени:
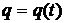 ,
,
зная которую, легко найти и 2 другие зависимости:
 в соответствии с определением электроемкости конденсатора
в соответствии с определением электроемкости конденсатора
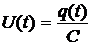
и по закону Ома для однородного участка цепи сопротивлением R
|
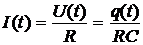 ,
,
откуда видно, что для нахождения закона изменения тока, текущего через сопротивление, необходимо определить закон убывания заряда на конденсаторе.
Пусть за малый промежуток времени dt заряд на конденсаторе уменьшится на величину dq. Весь этот заряд dq протечет за это время dt через сопротивление R (рис. 28). В соответствии с определением силы тока можно записать
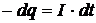 ,
,
где знак минус означает уменьшение.
В то же время сила тока подчиняется закону Ома, т.е. прямо пропорциональная текущему напряжению U на конденсаторе, которое в свою очередь связана с текущим значением заряда на нем в соответствии с определением емкости, т.е.
 .
.
Подставляем в предыдущее выражение:

– дифференциальное уравнение, описывающее процесс разрядки конденсатора. Его решение имеет вид
 .
.
Теперь легко получить и искомый закон изменения тока. Запишите его самостоятельно.
2) заряд q, прошедший через сопротивление за время t =2 мс, равен
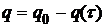 .
.
Вычислите самостоятельно.
3) Закон Джоуля-Ленца в виде
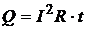
справедлив при  в течение всего времени t. В данном случае ток меняется по найденному закону, поэтому для нахождения количества теплоты Q, выделившегося в сопротивлении за время t =2 мс, воспользуемся законом Джоуля-Ленца в виде
в течение всего времени t. В данном случае ток меняется по найденному закону, поэтому для нахождения количества теплоты Q, выделившегося в сопротивлении за время t =2 мс, воспользуемся законом Джоуля-Ленца в виде
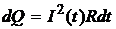 .
.
Подставим сюда найденный выше закон изменения тока

и проинтегрируем, получим определенный интеграл
 .
.
Вычислим этот интеграл в системе Mathcad:
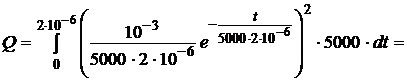 10-3 (Дж)=1 (мДж).
10-3 (Дж)=1 (мДж).
Не нашли, что искали? Воспользуйтесь поиском: