Методические указания к решению типовых задач. Задача №4.1. Два проводящих шара радиусами R1=8 см и R2=20 см находятся на большом расстоянии друг от друга и имеют заряды q1=14 нКл и q2= –7 нКл

Задача №4.1. Два проводящих шара радиусами R ₁=8 см и R ₂=20 см находятся на большом расстоянии друг от друга и имеют заряды q ₁=14 нКл и q ₂= –7 нКл. Каким станет заряд q ₂¢ (в нКл) второго шара, если шары соединить проводником? Емкостью соединительного проводника пренебречь. (4, с. 88)

Указания по решению. Заданные размеры шаров эквивалентны заданию их электроемкости (от вида вещества проводника его емкость не зависит).

Известно, что потенциал шара j связан с его зарядом q формулой

,

отсюда получаем выражение для электроемкости шара

,

где e - диэлектрическая проницаемость среды, в которой находится шар.

При соединении шаров происходит перераспределение заряда между ними до тех пор, пока потенциалы шаров не станут равны. При этом алгебраическая сумма заряда не меняется:

,

отсюда

. (*)

Постоянной остается и емкость каждого шара, т.е. отношение заряда к потенциалу:

и .

Составим отношение этих равенств

.

С другой стороны, из выражения емкости шара получаем

.

Приравняем правые части последних равенств:

,

и с учетом (*) имеем

,

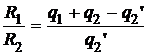откуда легко найти искомую величину.

Завершите самостоятельно решение задачи в общем виде и произведите вычисления.

Задача №4.2. Между обкладками изолированного плоского конденсатора, заряженного до разности потенциалов U ₁=400 В, находится пластина с диэлектрической проницаемостью e =5, примыкающая вплотную к обкладкам. Какова будет разность потенциалов U ₂ между обкладками конденсатора после удаления диэлектрика?

Указания по решению. В соответствии с формулой (4.3) емкость плоского конденсатора при удалении диэлектрика уменьшится в e раз. При этом заряд на его обкладках не изменится (зарядам некуда уйти). Тогда согласно формуле (4.2) напряжение увеличится в e раз.

Задача №4.3. Шар, погруженный в масло (e =2,2), имеет поверхностную плотность заряда s =1 мкКл/м² и потенциал j =500 В. Определите: 1) радиус шара R; 2) заряд шара q; 3) электроемкость шара C; 4) энергию шара W_p. [1) 9,74 мм; 2) 1,19 нКл; 3) 2,38 пФ; 4) 0,3 мкДж] (5, с. 84)

.

Потенциал шара в диэлектрике связан с его зарядом соотношением

.

С учетом предыдущего равенства получаем

,

откуда можно выразить искомый радиус шара:

.

В задаче 4.1 было получено выражение для емкости шара

.

Тогда с учетом выражения для радиуса шара получим в данном случае:

.

Энергию шара найдем по формуле (4.8):

.

Самостоятельно произведите расчеты и сравните полученные числовые значения искомых величин.

Задача №4.4. Найдите емкость С слоистого сферического конденсатора с радиусами обкладок R ₁=2 см и R ₂=2,6 см, между сферическим обкладками которого находятся два концентрических слоя диэлектрика, толщины и диэлектрические проницаемости которых равны соответственно d ₁= 0,2 см, d ₂= 0,4 см, e ₁=7, e ₂=2 (рис. 17).

Указания по решению. Емкость заданного конденсатора будем искать в соответствии с определением емкости конденсатора, т.е. по формуле (4.2):

,

где напряжение следует искать из связи между напряженностью электрического поля конденсатора и разностью потенциалов. Учитывая сферическую симметрию поля конденсатора, получим указанную связь в виде

,

где интегрирование должно проводиться от одной обкладки конденсатора до другой вдоль радиального направления.

Остается найти закон изменения величины напряженности поля 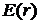между сферическими обкладками данного конденсатора.

Т.к. среда диэлектрическая и неоднородная, то воспользуемся теоремой Гаусса для вектора электрического смещения (постулатом Максвелла):

,

где q – свободный заряд внутри замкнутой поверхности S.

Практический аспект постулата Максвелла состоит в том, что с его помощью рассчитываются симметричные элект­рические поля в неоднородных средах.

,

здесь q – заряд обкладки конденсатора (заряд меньшей сферы).

Тогда получаем выражение для смещения:

, R ₁ £ r £ R ₂.

Эта формула действует в обоих диэлектрических слоях.

Далее из формулы связи вектора электрического смещения с вектором напряженности поля получим формулы для напряженностей в слоях диэлектриков:

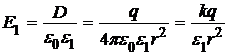, R ₁ £ r £ R ₁+ d ₁.

, R ₁+ d ₁ £ r £ R ₂.

При переходе через границу раздела между слоями напряженность испытывает разрыв, обусловлен­ный наличием на этой границе поверхностного связан­ного заряда. Поэтому при подстановке в эти выражения r = R ₁+ d ₁ напряженности не совпадают, и их разность даст скачок напряжен­ности при переходе через границу.

Далее выразим напряжение на конденсаторе, исполь­зуя в качестве линии интегрирования радиальную пря­мую, соединяющую обкладки. Поскольку эта прямая проходит через оба диэлектрических слоя, в каждом из которых действует своя формула напряженности, интеграл разбивается на сумму двух интегралов:

Отсюда находим емкость сферического двухслойного конденсатора:

.

Вычислим:

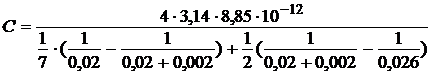=2,682×10^-11 (Ф)=

=26,82 (пФ).

Самостоятельно получите из общей формулы решения этой задачи формулу для емкости сферического конденсатора с однородным диэлектриком между обкладками. Сравните полученное выражение с формулой емкости плоского конденсатора.

Задача №4.5. Найдите электрическую энергию системы 4-х зарядов q, 2 q, 3 q и – q, расположенных в вершинах квадрата со стороной а (рис. 18).

Указания по решению. Энергия системы зарядов определяется формулой (4.4).

1) Найдем потенциалы ЭСП в вершинах квадрата на основе принципа суперпозиции:

, ,

.

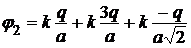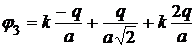2) Энергия их взаимодействия равна

.

Самостоятельно проведите подстановку выражений для потенциалов и получите окончательный ответ в общем виде.

Задача №4.6. Найдите электрическую энергию непрерывно распределенного по объему шара заряда с объемной плотностью r_q. Принять, что диэлектрическая среда отсутствует.

Указания по решению. Энергию распределенного по объему заряда найдем по формуле (4.5):

.

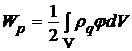Здесь j - потенциал поля в точках шара, т.е. задается формулой (см. задачу 3.2):

, .

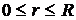С учетом сферической симметрии в качестве элементов объема следует выбрать тонкие сферические слои толщиной dr. В каждой точке такого слоя потенциал одинаков. Тогда элементарный объем

.

Подставляем:

.

После преобразований получим

.

Задача №4.7. Электрическое поле создано равномерно заряженным с объемной плотностью шаром радиуса R. Найдите объемную плотность энергии электрического поля во внутренней и внешней области. Диэлектрическая среда отсутствует.

Указания по решению. Объемная плотность энергии электрического поля задается в соответствии с (4.10) формулой:

при e =1.

В задаче 3.2 были получены выражения для напряженности поля внутри и вне объемно заряженного шара:

при

и

при .

Соответственно получаем выражения для плотности энергии:

внутри шара

и

вне шара.

Самостоятельно получите аналогичным образом выражения для плотности энергии поля при наличии диэлектрической среды с проницаемостью e. Сравните полученные выражения и сделайте соответствующий вывод.

Задача №4.8. Электрическое поле создано равномерно заряженным с объемной плотностью шаром радиуса R. 1) Найдите энергию электрического поля, заключенного во внутренней и внешней области пространства. Диэлектрическая среда отсутствует. 2) Найдите суммарную энергию поля и сравните с энергией взаимодействия распределенного по объему шара заряда.

Указания по решению. Воспользуемся формулой (4.9), учитывая результаты, полученные в ходе решения предыдущей задачи. Энергию поля найдем суммированием энергии элементарных сферических слоев объемом .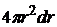

1) Энергия поля внутри шара

или

.

2) Энергия поля вне шара

или

.

Суммарная энергия поля внешней и внутренней областей равна

.

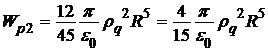Сравнивая эту формулу с результатом, полученным в задаче 4.5, убеждаемся в их полном совпадении.

В связи с этим заметим, что в электростатике оба подхода в нахождении электрической энергии равноправны. Это обусловлено тем, что электростатические поля и их источники – неподвижные заряды – существуют всегда совместно и взаимосвязаны между собой основными формулами электростатики.

Задача №4.9. Воспользовавшись выражением для плотности энергии электрического поля, выразите энергию плоского конденсатора через: 1) заряд Q на обкладках; 2) через напряжение U между обкладками. Найдите силу притяжения обкладок друг к другу в каждом из этих случаев.

Указания по решению. Плотность энергии электрического поля равна

.

считаем, что все поле заключено в пространстве между обкладками, т.е. занимает объем

,

где S – площадь обкладки, d – расстояние между обкладками конденсатора.

Получаем

.

Напряженность поля конденсатора связана с напряжением между обкладками

.

Тогда

.

Электроемкость плоского конденсатора

,

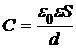тогда

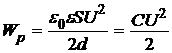
– выражение для энергии конденсатора через напряжение между его обкладками.

С учетом определения емкости конденсатора

,

получаем

.

Иначе можно записать

– выражение для энергии конденсатора через заряд на обкладках.

Наконец, силу притяжения пластин найдем согласно равенствам:

.

1) Имеем

Þ .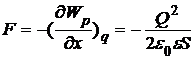

2) Имеем

Þ .

Отметим, что знак «-» соответствует тому, что пластины притягиваются друг к другу (т.е. силы притяжения считаются отрицательными, а силы отталкивания – положительными).

Задача №4.10. Найдите работу, совершенную внешними силами по зарядке сферы радиусом R до заряда Q.

Указания по решению. Элементарная работа при перемещении заряда dq ¢ из бесконечности () на сферу равна

.

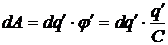Интегрируем по заряду сферы

.

Сравнивая с формулой для энергии заряженного проводника, можно сделать вывод, что работа по зарядке сферы переходит в потенциальную энергию заряженной сферы.

Не нашли, что искали? Воспользуйтесь поиском: