Некоторые замечания к теоретическому материалу. Теорема Гаусса-Остроградского утверждает, что поток вектора напряженности электрического поляФЕсквозь произвольную замкнутую поверхностьSв однородной

Теорема Гаусса-Остроградского утверждает, что поток вектора напряженности 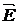электрического поля Ф _Е сквозь произвольную замкнутую поверхность S в однородной изотропной и линейной среде пропорцио­нален электрическому заряду q , заключенному внутри поверхности. В системе СИ коэффициент пропорцио­нальности равен .

В интегральной форме теорема может быть пред­ставлена в виде:

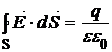. (3.1)

Для практического применения формулы (1) важно выбирать в качестве поверхности интегрирования S поверхность, для которой верны следующие условия:

Иногда удается выбрать поверхность, в одной части которой выполнены указанные условия (*), а поток вектора сквозь другую часть поверхности равен нулю (линии напряженности параллельны этой поверхности, т.е. не пересекают ее).

В случае выполнения условий (*) интеграл становится равен

,

где S – площадь выбранной замкнутой поверхности S, т.е. значение интеграла становится равным произведению значения напряженности поля в точках поверхности на площадь этой поверхности. Искомое значение напряженности тогда будет находиться из равенства

(3.2)

Постулат Мак­свелла в интегральной форме: поток вектора смещения через замкнутую поверхность в произвольной среде равен свободному заряду, заключенному внутри поверхности. Это записывается в виде:

(3.3)

или, если свободный заряд распределен по объему V, ограниченному поверхностью S, с объемной плотностью r_q:

(3.3¢)

По отношению к этому постулату теорема Гаусса-Остроградского выступает как частный случай, соответствующий однородной среде и статическим полям.

Под действием внешнего поля молекулы диэлектрика приобретают дипольный момент. Суммарный дипольный момент единицы объема определяет макроскопическую характеристику свойства диэлектрика «поляризоваться во внешнем электрическом поле», называемую вектором поляризации или поляризованностью:

. (3.4)

Вектор поляризации связан с напряженностью электрического поля в диэлектрике. В случае линейной изотропной среды

, (3.5)

где – диэлектрическая восприимчивость вещества, связанная с его диэлектрической проницаемостью соотношением

. (3.6)

В случае однородной поляризации связанные заряды диэлектрика распределены только по его поверхности. Поверхностная плотность поляризационных (связанных) зарядов численно равна нормальной составляющей вектора поляризации:

. (3.7)

При решении задач, требующих нахождения поверхностной плотности связанных зарядов диэлектрика, необходимо:

1) найти напряженность 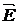электрического поля в диэлектрике (используя, например, теорему Гаусса или постулат Максвелла и т.д., или воспользовавшись готовой формулой из таблицы приложения 3);

2) найти поляризованность диэлектрика по формуле (3.5) с учетом (3.6);

3) зная направление вектора поляризации относительно поверхности диэлектрика, найти его нормальную составляющую;

4) воспользоваться формулой (3.7) для вычисления поверхностной плотности связанных зарядов.

Не нашли, что искали? Воспользуйтесь поиском: