
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Градиент скалярной функции–это вектор, направленный в каждой точке в сторону наиболее быстрого возрастания функции, равный по модулю производной от функции по этому направлению.
Разделив обе части (2.1) на заряд и учитывая (1.2), получим формулу связи между напряженностью и потенциалом электрического поля:
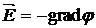 (2.2)
(2.2)
Знак минус в (2.2) указывает на то, что вектор напряженности ориентирован в направлении наиболее быстрого убывания потенциала.
В одномерном случае в прямоугольной декартовой системе координат формула (2.2) имеет вид:
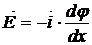 (2.3)
(2.3)
В одномерных полях сферической симметрии:
 . (2.4)
. (2.4)
Перейдя к скалярной форме записи выражения (2.4) и представив в виде 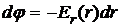 , преобразуем его следующим образом:
, преобразуем его следующим образом:
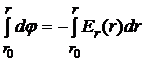 или
или  . (2.5)
. (2.5)
Если в качестве r 0 принять радиальную координату нулевой точки, для которой j (r 0)=0, то тогда последнее соотношение примет вид:
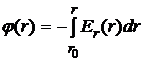 (2.6)
(2.6)
Формула (2.6) используется для определения потенциала j (r) по ранее найденной напряженности Е (r).
Для полей плоской симметрии справедливы формулы (2.5) и (2.6) с заменой в них r на х и r 0 на х0, где х0 – координата плоскости, в точках которой потенциал принят равным нулю.
Среда называется линейной, если ее проницаемость e не зависит от напряженности созданного в ней электрического поля. Для электрических полей в вакууме и в линейных средах выполняется принцип суперпозиции: если в линейной среде создано несколько электрических полей, то результирующая напряженность равна векторной сумме напряженностей, а результирующий потенциал — скалярной (алгебраической [3]) сумме потенциалов всех полей:
 ,
,  (2.7)
(2.7)
Принцип суперпозиции отражает тот факт, что в линейных средах электрические поля не взаимодействуют между собой, а просто накладываются друг на друга.
Принцип суперпозиции лежит в основе метода расчета электрических полей, создаваемых заряженными телами. Сущность метода состоит в том, что тело, выступающее как источник поля, представляется разделенным на элементы, размеры которых достаточно малы, чтобы в рассматриваемой задаче их можно было считать точечными зарядами. Применив к отдельному элементу формулу, описывающую поле точесного заряда, получают выражение для потенциала dj поля, создаваемого в точке наблюдения этим элементом. Затем это выражение интегрируется по всем элементам источника поля, в результате чего получается полный потенциал в точке наблюдения. Расчет поля завершается определением напряженности по найденному потенциалу с помощью формулы (2.2).
Возможен и обратный подход к расчету поля, когда с помощью принципа суперпозиции рассчитывается напряженность, а затем по найденной напряженности с помощью формулы типа (2.5) определяется потенциал. В большинстве случаев, однако, предпочтительней первый подход, ибо при втором подходе принцип суперпозиции приводит в общем случае к более сложному векторному интегралу для напряженности по сравнению со скалярным интегралом для потенциала при первом подходе. Однако в любом случае исходными являются формулы для напряженности Е и потенциала j полей точечных зарядов.
Не нашли, что искали? Воспользуйтесь поиском: