
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методические указания к решению типовых задач. Задача №1.1. Как изменится сила взаимодействия двух металлических заряженных шариков, если их привести в соприкосновение
Задача №1.1. Как изменится сила взаимодействия двух металлических заряженных шариков, если их привести в соприкосновение, а затем удалить на прежнее расстояние?
Указания по решению. В задаче требуется сравнить 2 силы взаимодействия заряженных тел в двух случаях. Обозначим их  и
и  . Величины этих сил зависят от величин зарядов шариков и от расстояния между ними (см. закон Кулона), а направления от совпадения или не совпадения знаков этих зарядов[1].
. Величины этих сил зависят от величин зарядов шариков и от расстояния между ними (см. закон Кулона), а направления от совпадения или не совпадения знаков этих зарядов[1].
Возможны следующие случаи (см. таблицу 1):
Таблица 1
| Заряды шариков | Расстояние между шариками | Сила взаимодействия | |||||
| до соприкосновения | после соприкосновения | величина | направление | ||||
| до соприкосновения | после соприкосновения | до соприкосновения | после соприкосновения | ||||
| I случай | одноименные, равные  и и 
| одноименные,
равные

| не меняется | 
| 
| оттал-кивание | оттал-кивание |
| II случай | разноименные, равные  и и 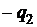
| одноименные,
равные
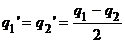
| 
| 
| притя-жение | оттал-кивание |
Сравнение сил сводится к сравнению величин[2]  и
и  .
.
Завершите сравнение самостоятельно и дайте ответ к задаче.
Задача №1.2. В некоторой точке поля на заряд q действует сила F. Найдите напряженность поля в этой точке и определите заряд, создающий поле, если точка от него удалена на расстояние r.
Указания по решению. По определению напряженность электрического поля есть вектор
 ,
,
модуль которого равен
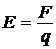 ,
,
а направление совпадает с направлением силы, действующей на заряд, если заряд положителен, и противоположно направлению силы, если заряд отрицателен.
Считая, что поле создано точечным зарядом Q, получим
 Þ
Þ 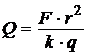 .
.
Подумайте: зависит ли искомая величина заряда Q, создающего поле, от величины данного в задаче заряда q? Почему?
Задача №1.3. Два заряда q 1и q 2 расположены в керосине на расстоянии r друг от друга. Найдите, пользуясь определением, напряженность поля в середине отрезка, соединяющего центры зарядов.
Указания по решению. Представим, что в середине отрезка, соединяющего центры зарядов, находится положительный заряд q. На него будут действовать 2 кулоновские силы, со стороны зарядов q 1и q 2. Результирующая этих сил равна
 .
.
Результирующая сила согласно закону Кулона будет направлена вдоль оси х, а ее проекция на эту ось будет равна
 ,
,
 где e – диэлектрическая проницаемость керосина.
где e – диэлектрическая проницаемость керосина.
|
 .
.
Направление вектора  определяется знаком большего по модулю заряда.
определяется знаком большего по модулю заряда.
Самостоятельно рассмотрите возможные случаи направления вектора напряженности в зависимости от значений и знаков данных зарядов q 1и q 2.
Задача №1.4. Металлический шар радиусом R =5 см заряжен до потенциала j =150 В. Чему равна напряженность поля в точке, находящейся на расстоянии r =5 см от поверхности шара?
|
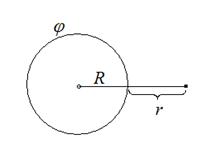 Указания по решению. Процесс зарядки проводника, распределение заряда по поверхности проводника и т.д. будут рассматриваться при изучении понятия электроемкости. Вывод формулы для напряженности и потенциала заряженной сферы (шара) также будет осуществлен позднее (при рассмотрении принципа суперпозиции или теоремы Остроградского-Гаусса). Здесь же отметим лишь, что электрическое поле заряженного шара (сферы) во внешней области аналогично полю точечного заряда, расположенного в точке, совпадающей с центром шара.
Указания по решению. Процесс зарядки проводника, распределение заряда по поверхности проводника и т.д. будут рассматриваться при изучении понятия электроемкости. Вывод формулы для напряженности и потенциала заряженной сферы (шара) также будет осуществлен позднее (при рассмотрении принципа суперпозиции или теоремы Остроградского-Гаусса). Здесь же отметим лишь, что электрическое поле заряженного шара (сферы) во внешней области аналогично полю точечного заряда, расположенного в точке, совпадающей с центром шара.
Имеем следующие формулы:
- для потенциала поля шара (сферы) в точке на расстоянии r от поверхности шара:
 ,
,
тогда при r =0 получаем потенциал шара  (потенциал на поверхности шара одинаков во всех точках – свойство проводника);
(потенциал на поверхности шара одинаков во всех точках – свойство проводника);
- для величины напряженности
 ,
,
где R – радиус шара.
Выражая заряд шара через его потенциал и подставляя в формулу для напряженности, получим искомую величину:
 .
.
Самостоятельно проведите вычисления и запишите ответ, указав единицы измерения.
Задача №1.5. Протон, движущийся со скоростью v 0=100 км/с, влетает в электрическое поле с напряженностью Е =50 В/м в направлении, противоположном направлению силовых линий поля. Какую разность потенциалов пройдет протон до полной остановки? Через сколько микросекунд скорость протона станет равной нулю? Отношение заряда протона к его массе равно  =108 Кл/кг.
=108 Кл/кг.

 Указания по решению. Протон – частица, несущая положительный заряд. Со стороны электрического поля на нее действует сила в направлении силовых линий. В данном случае эта сила направлена противоположно скорости частицы, поэтому скорость протона будет уменьшаться по мере его движения в поле до нуля, а затем начнется движение в противоположном начальному направлении. В этом усматривается аналогия с движением тела, брошенного вверх в поле тяготения Земли. Электростатическое поле, как и гравитационное, потенциально: заряженная частица обладает в этом поле потенциальной энергией.
Указания по решению. Протон – частица, несущая положительный заряд. Со стороны электрического поля на нее действует сила в направлении силовых линий. В данном случае эта сила направлена противоположно скорости частицы, поэтому скорость протона будет уменьшаться по мере его движения в поле до нуля, а затем начнется движение в противоположном начальному направлении. В этом усматривается аналогия с движением тела, брошенного вверх в поле тяготения Земли. Электростатическое поле, как и гравитационное, потенциально: заряженная частица обладает в этом поле потенциальной энергией.
При движении протона в ЭСП на него не действуют непотенциальные силы, поэтому выполняется закон сохранения полной механической энергии. Отсюда следует, что в положениях 1 и 2 суммы кинетической и потенциальной энергии протона равны между собой:
 ,
,
 Þ
Þ  .
.
А искомая разность потенциалов равна
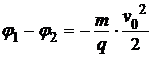 .
.
Знак «–» означает. что протон движется в сторону большего потенциала.
Рассмотренное выше рассуждение широко применяется при использовании понятия ускоряющей разности потенциалов.
Заметим, что физический смысл имеет не само значение потенциала, а разность потенциалов между двумя точками, что и отражено в приведенных выше рассуждениях. А значение потенциала в некоторой точке определяется, в соответствии с этим, лишь относительно другой точки, выбранной в качестве нулевой (значение потенциала в которой условно принимается равным нулю).
Для ответа на второй вопрос задачи рассмотрим равнозамедленное движение протона под действием электрической силы  . По второму закону Ньютона для протона ускорение равно
. По второму закону Ньютона для протона ускорение равно
 .
.
Зависимость модуля скорости от времени при равнозамедленном движении имеет вид
 ,
,
тогда  при
при  . Подставляя выражение для ускорения, получаем искомое время:
. Подставляя выражение для ускорения, получаем искомое время:
 .
.
Вычисления проведите самостоятельно и сделайте проверку размерностей.
Задача №1.6. При переносе точечного заряда q =10 нКл из бесконечности в точку, находящуюся на расстоянии r =20 см от поверхности равномерно заряженного шара, необходимо совершить работу A =0,5 мкДж. Радиус шара R =4 см. Найдите потенциал j на поверхности шара и плотность распределения заряда. Потенциал на бесконечности принять равным нулю.
Указания по решению. Как уже отмечалось в задаче №1.4 поле равномерно заряженного шара описывается формулами поля точечного заряда, т.е. потенциал поля в точке на расстоянии r от поверхности шара радиусом R равен
 ,
,
где Q – заряд шара, равный в случае равномерного распределения заряда по объему шара с объемной плотностью 
 . (1.1)
. (1.1)
С учетом (1.1) потенциал поля шара запишется в виде
 .
.
Известно из механики, что работа потенциальной силы равна убыли потенциальной энергии [8, с. 89]. В данном случае потенциальной силой является сила, с которой электростатическое поле, созданное зарядом Q, действует на точечный заряд q. В условии задачи речь идет о работе внешних сил, по преодолению этой потенциальной силы. Поэтому работа внешних сил равна приращению потенциальной энергии точечного заряда q в поле заряда Q, т.е.
 ,
,
где потенциал на бесконечности принят равным нулю 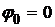 , а j - потенциал в точке на расстоянии r от поверхности шара. Отсюда, подставляя выражение для потенциала, можно выразить искомую плотность распределения заряда.
, а j - потенциал в точке на расстоянии r от поверхности шара. Отсюда, подставляя выражение для потенциала, можно выразить искомую плотность распределения заряда.
Потенциал на поверхности шара находится аналогично тому, как показано в задаче №1.4.
Завершите решение задачи самостоятельно (см. приложение 7).
Задача №1.7. ЭСП создается положительно заряженной с постоянной поверхностной плотностью s = 10 нКл/м2 бесконечной плоскостью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r 1=2 см до r 2=1 см? [9,04×10-19 Дж] (4, с. 128)
Указания по решению. Положительно заряженная бесконечная плоскость создает электрическое поле, линии напряженности которого указаны на рис. 4.
|

Электрон – отрицательно заряженная частица, поэтому в электрическом поле он будет двигаться против силовых линий (что соответствует притяжению разноименных зарядов). Поэтому при перемещении электрона вдоль силовой линии с большего на меньшее расстояние от плоскости работа внешних сил будет отрицательной и численно равной изменению потенциальной энергии электрона в электрическом поле плоскости:
 .
.
Разность потенциалов между двумя точками поля бесконечной плоскости равна (см. приложение 3)
 ,
,
подставляем и получаем выражение для искомой величины:
 ,
,
где е – элементарный заряд (см. приложение 4).
Произведите вычисления самостоятельно и сравните ответ.
Задача №1.8. Два заряда – q и 9 q находятся на расстоянии d друг от друга. Со стороны отрицательного заряда по линии, проходящей через эти заряды, движется по направлению к ним заряд q. Какой минимальной кинетической энергией он должен обладать на бесконечности, чтобы попасть в точку, где находится отрицательный заряд?
Указания по решению. На движущийся заряд q со стороны двух неподвижных зарядов – q и 9 q действуют две кулоновские силы  и
и  : со стороны отрицательного заряда – сила притяжения
: со стороны отрицательного заряда – сила притяжения  , а со стороны положительного – сила отталкивания
, а со стороны положительного – сила отталкивания  . т.е. эти силы противоположно направлены. Определим направление результирующей силы. Для этого сравним величины сил, определяемые законом Кулона:
. т.е. эти силы противоположно направлены. Определим направление результирующей силы. Для этого сравним величины сил, определяемые законом Кулона:

и
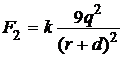 .
.
Из равенства

найдем точку, в которой результирующая сила равна нулю. Получаем:
 ,
,
 ,
,
 ,
,
отсюда
 .
.
 Это расстояние на рис. 5 помечено точкой О. До точки О на движущийся заряд действует результирующая сила отталкивания, а после результирующая сила становится силой притяжения. Следовательно, достаточно этому заряду достичь точки О, чтобы он далее попал в место нахождения отрицательного заряда.
Это расстояние на рис. 5 помечено точкой О. До точки О на движущийся заряд действует результирующая сила отталкивания, а после результирующая сила становится силой притяжения. Следовательно, достаточно этому заряду достичь точки О, чтобы он далее попал в место нахождения отрицательного заряда.
|
 , тогда в точке О он будет иметь скорость, равную нулю. Далее проводим рассуждения, описанные в задаче №1.5. Получаем из закона сохранения энергии:
, тогда в точке О он будет иметь скорость, равную нулю. Далее проводим рассуждения, описанные в задаче №1.5. Получаем из закона сохранения энергии:
 .
.
где  - потенциал электрического поля в точке О, созданного двумя зарядами – q и 9 q.
- потенциал электрического поля в точке О, созданного двумя зарядами – q и 9 q.
Для завершения решения этой задачи необходимо применение принципа суперпозиции электрических полей, который рассматривается в теме следующего практического занятия.
Не нашли, что искали? Воспользуйтесь поиском: