Методические указания к решению типовых задач.

Задача №3.1. Напряженность однородного электрического поля равна Е. Чему равен поток напряженности электрического поля через квадрат со стороной а, плоскость которого расположена под углом j =30⁰ к направлению электрического поля. [ ] (6, с. 191)

Указания по решению. По определению поток напряженности электрического поля равен

,

где a - угол между нормалью к плоскости квадрата и вектором . Из рис. 11 видно, что

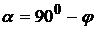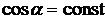Так поле по условию однородно, то и во всех точках поверхности квадрата, т.е. их можно вынести за знак интеграла, получаем:

.

Интеграл по поверхности равен площади этой поверхности, в данном случае это – площадь квадрата. Окончательно имеем:

.

Подумайте самостоятельно, при каких значениях угла j указанный поток будет иметь наибольшее и наименьшее значения.

Задача №3.2. Точечный заряд q =24 нКл расположен: 1) в центре куба; 2) в вершине куба; 3) в точке, симметричной центру куба, относительно одной из его граней. Определите поток вектора напряженности электрического поля данного заряда через: а) ближайшую к заряду грань куба, б) поверхность куба. ребро куба равно а =2 м.

Указания по решению. По определению поток вектора через поверхность S равен

, (3.8)

где Е_n – проекция вектора на нормаль к поверхности в данной точке[4].

Рассмотрим каждый из случаев по отдельности.

Для вычисления поверхностного интеграла (3.8) выберем декартову систему координат так: начало координат поместим в центр куба, а координатные оси проведем параллельно трем взаимно перпендикулярным ребрам куба (рис. 12).

Далее учтем, что в силу симметрии поток через верхнюю грань в 4 раза больше потока через ее заштрихованную часть S₁– квадрат со стороной .

Получаем

.

Вектора и направлены по оси z.

Имеем для величины напряженности поля точечного заряда

,

кроме того, из геометрических соображений по рис.12

, .

Подставляем:

.

Подставляем числовые данные и вычисляем в системе Mathcad:

(Н×м²/Кл).

Соответственно поток через всю поверхность куба в 6 раз больше.

2) Если заряд расположен в вершине куба, то поток вектора напряженности через грани, которым принадлежит эта вершина, равен нулю (таких граней три). А потоки через другие 3 грани равны между собой.

Аналогично предыдущему имеем:

.

Вычисляем:

(Н×м²/Кл).

Тогда поток через всю поверхность куба будет в 3 раза больше.

Подумайте, сравнивая числовые значения в рассмотренных двух случаях, почему так велика разница?

3) Если заряд, создающий поле, поток которого вычисляется, расположен вне замкнутой поверхности, то поток вектора напряженности через эту поверхность всегда равен нулю, независимо от конкретного положения заряда по отношению к поверхности.

Задача №3.3. Поток напряженности электрического поля через плоскую поверхность, равномерно заряженную с поверхностной плотностью заряда s, равен F. Чему равна электрическая сила, действующая на пластину в направлении, перпендикулярном ее плоскости? (6, с. 192) [ ]

Указания по решению. Заметим, что в условии не сказано, что задан поток однородного электрического поля. Поэтому считаем, что поле не однородно. Обозначим S – площадь данной плоской поверхности S₀[5], тогда поток через элемент плоской поверхности в некоторой точке поля равен

,

а суммарный поток, данный в условии задачи, есть

.

Элемент поверхности площадью dS несет заряд

,

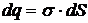на который действует нормальная к поверхности электрическая сила

.

Чтобы найти суммарную силу, действующую на всю пластину в направлении, перпендикулярном ее плоскости, необходимо проинтегрировать последнее выражение по поверхности пластины, т.е.

.

Задача №3.4. Две концентрично расположенные тонкостенные металлические сферы имеют радиусы R ₁=15 см и R ₂=25 см. Внутри объема, ограниченного первой сферой, распределен заряд с плотностью r_q =-1,10×10^-8 Кл/м³. Внешняя сфера имеет заряд Q ₂=2,71×10^-7 Кл. Точки А, В, С расположены на расстояниях r_А =10 см, r_В =18 см, r_С =40 см от центра сфер. Определите напряженность поля в этих точках и постройте график зависимости E = f (r).

Указания по решению. Для решения задачи необходимо применить теорему Гаусса-Остроградского для вектора напряженности электростатического поля:

,

где Q – суммарный заряд внутри замкнутой поверхности S.

1) Точка А лежит внутри сферы R ₁. В качестве поверхности выберем S выберем сферу радиуса r_А. В силу симметрии напряженность поля во всех точках на поверхности S будет одинакова, поэтому теорема Гаусса-Остроградского запишется так:

,

где заряд внутри сферы радиуса r_А найден по определению объемной плотности распределения заряда при условии, что =const.

Отсюда выражаем искомое значение Е_А:

.

Вычисляем:

41,431 (В/м).

Т.к. по объему распределен отрицательный заряд, то в точке А напряженность направлена к центру сфер.

2) Точка В лежит между сферами R ₁ и R ₂. В качестве поверхности выберем S выберем сферы радиуса r_В. В силу симметрии напряженность поля во всех точках на поверхности S также будет одинакова. Внутри этой замкнутой поверхности будет находиться полный заряд, распределенный внутри сферы R ₁, т.е. теорема Гаусса-Остроградского запишется так:

.

Отсюда выражаем искомое значение Е_В:

, e =1.

Вычисляем:

43,158 (В/м).

В точке В напряженность также направлена к центру сфер.

3) Точка С лежит вне сферы R ₂. В качестве поверхности выберем S выберем сферы радиуса r_С. В силу симметрии напряженность поля во всех точках на поверхности S также будет одинакова. Внутри этой замкнутой поверхности будет находиться полный заряд, распределенный внутри сферы R ₁, и весь заряд Q ₂, т.е. теорема Гаусса-Остроградского запишется так:

.

Здесь важно учесть противоположность знаков слагаемых зарядов.

Отсюда выражаем искомое значение Е_С:

, e =1.

Вычисляем:

=1,524×10⁴ (В/м).

В точке С напряженность также направлена от центра сфер.

Построим график зависимости Е (r) в системе Mathcad (рис. 14):

Задача №3.5. Шар радиуса R равномерно заряжен с объемной плотностью заряда r_q. С помощью теоремы Гаусса-Остроградского найдите напряженность поля внутри и вне шара. Нуле­вую точку выберите в бес­конечности и найдите зависимость j (r) потенциала поля от расстояния r до центра шара. Постройте графики зависимостей Е (r) и j (r).

Указания по решению. В ходе решения предполагается линей­ность, одно­родность и изотропность свойств среды. Поэтому заданное поле обладает сферической симметрией, и его характеристики (напряженность и потен­циал) зависят лишь от расстояния до центра шара.

Внутренняя задача. В качестве замкнутой поверхности выбираем сферу радиуса . Внутри этой поверхности будет находиться заряд, объемно распределенный по шару такого же радиуса, т.е.

.

Т.к. выбранная поверхность удовлетворяет условиям (*) (в силу симметрии вектор напряженности во всех точках сферы перпендикулярен к ней и одина­ков по величине), то искомая напряженность внутри объемно заряженного шара находится из равенства

Þ

при .

Здесь принято e =1, т.е. диэлектрическая среда отсутствует.

Внешняя задача. В качестве замкнутой поверхности выбираем сферу радиуса . Особенность внешней задачи в том, что при любом заряд внутри вспомогательной сферы один и тот же, он равен полному заряду шара:

.

Аналогично, получаем

Þ при .

Полученные результаты изображены графически на рис. 15.

Для определения по­тенциала по найденной на­пряженности используем соотношение (2.6). Нуле­вую точку выбираем в бес­конечности. В качестве линии интегрирования выбираем радиальную прямую, соединяющую центр шара с бесконечно удаленной точкой.

Для определения потенциала j ₁ во внутренней области интегрирование проводится вдоль всей прямой, т. е. через две области с разными формулами напряженности. Поэтому интеграл разбива­ется на сумму двух интегралов:

.

Выполнив интегрирование и подставив пределы, полу­чим потенциал внутренних точек:

при .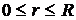

Для внешних точек вся линия интегрирования про­ходит только по одной внешней области с формулой напряженности . Поэтому потенциал выражается только одним интегралом:

.

Для потенциала внешних точек получаем:

при .

На рис. 15 зависимости Е (r) для внутренней (1) и внешней (2) областей представлены нижней линией; верхняя линия представляет зависимость j (r).

Отметим, что на границе шара, т. е. при r =R формулы для внутренних и внешних характеристик должны давать одинаковые значения Е (точка а) и j (точка b), что можно использовать для проверки правильности полученных решений.

Задача №3.6. Свободные заряды равномерно распределены с объемной плотностью =5 нКл/м³ по шару радиусом R =10 см из однородного изотропного диэлектрика с проницаемостью e =5. Определите напряженность ЭСП на расстояниях r ₁= 5 см и r ₂= 15 см от центра шара. [1,88 В/м, 8,37 В/м] (5, с. 81)

Указания по решению. При наличии диэлектрической среды величина напряженности электрического поля претерпевает скачек на границе раздела сред (поверхность шара). Поэтому в таком случае удобнее рассматривать вектор электрического смещения и воспользоваться постулатом Максвелла:

,

где - объемная плотность распределения свободных зарядов.

Внутреняя задача. В качестве замкнутой поверхности выбираем сферу радиуса . Внутри этой поверхности будет находиться свободный заряд, объемно распределенный по шару такого же радиуса, т.е.

.

Т.к. выбранная поверхность удовлетворяет условиям (*) (в силу симметрии вектор электрического смещения во всех точках сферы перпендикулярен к ней и одина­ков по величине), то постулат Максвелла запишется в виде:

Þ

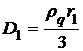при .

Далее используем формулу связи между значениями векторов напряженности и электрического смещения ЭСП:

.

Тогда для внутренней точки получаем

при .

Внешняя задача. В качестве замкнутой поверхности выбираем сферу радиуса . Особенность внешней задачи в том, что при любом свободныйзаряд внутри вспомогательной сферы один и тот же, он равен суммарному свободному заряду шара радиуса R:

.

Аналогично, получаем

Þ

при .

Аналогично, напряженность поля во внешней точке

при .

здесь учли, что e =1, т.к. по условию вне шара диэлектрическая среда отсутствует.

Проведите вычисления самостоятельно и сравните ответ.

Задача №3.7. Пространство между пластинами плоского конденсатора заполнено стеклом (e =7). Расстояние между пластинами d =5 мм, разность потенциалов U =1 кВ. Определите: 1) напряженность поля в стекле; 2) поверхностную плотность заряда на пластинах конденсатора; 3) поверхностную плотность связанных зарядов на стекле. [1) 200 кВ/м; 2) 12,4 мкКл/м²; 3) 10,6 мкКл/м²] (4, с. 81)

Указания по решению. 1) Зная связь напряженности поля с разностью потенциалов

,

найдем напряженность поля между пластинами конденсатора

.

2) Из приложения (2) воспользуемся формулой напряженности поля плоскости

.

Т.к. в конденсаторе имеется 2 пластины, которые разноименно заряжены, то в пространстве между ними поле будет в 2 раза больше, т.е. напряженность поля между пластинами конденсатора равно

Þ .

3) Поверхностная плотность связанных зарядов численно равна величине вектора поляризации среды

.

Завершите решение самостоятельно и проведите вычисления. Сравните полученные результаты.

Задача №3.8. Найдите плотности поляриза­ционных связанных зарядов на поверхностях диэлектри­ческого слоя между обкладками сферического конденса­тора с радиусами R _lи R ₂ (R ₁ < R ₂ ). Конденсатор заряжен до напряжения U. Диэлектрическая проницаемость слоя равна e. (1, с. 235)

Указания по решению. На обкладках конденсатора находятся равные по величине и противополож­ные по знаку заряды. В сферическом конденсаторе элек­трическое поле между обкладками создается действием только внутренней обкладки. Роль внешней обкладки сводится к компенсации поля внутренней обкладки во внешнем пространстве, за пределами конденсатора.

Поле равномерно заряженной сферы во внешнем пространстве аналогично полю точечного заряда (равного суммарному заряду Q сферы), находящегося в центре сферы:

,

где .

Выразим заряд сферического конденсатора через напряжение между обкладками:

Þ .

Тогда выражение для напряженности поля перепишется в виде:

.

Вектор напряженности направлен вдоль радиальных прямых от положительной обкладки к отрицательной. Также будет направлен и вектор поляризации диэлектрика, равный в любой точке диэлектрика

.

Тогда на меньшей поверхности диэлектрика, т.е. при , плотность поляризационных зарядов равна

,

а на большей поверхности диэлектрика, т.е. при 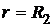, плотность поляризационных зарядов равна

.

Причем одно из выражений должно быть со знаком «+», а другое со знаком «-», что означает противоположность зарядов на обкладках конденсатора.

Заметим, что т.к. величины зарядов одинаковы, а площади, по которым они распределены разные, то различны и значения плотностей зарядов.

Правильность расчетов можно проверить согласно равенству

.

Кроме того, равенство суммарных поверхностных зарядов на диэлектрике означает отсутствие объемных связанных зарядов, т.е. то, что поляризация диэлектрика однородна.

Самостоятельно убедитесь в выполнении последнего равенства в данной задаче.

Не нашли, что искали? Воспользуйтесь поиском: