Закон Ома. Работа в цепи электрического тока. Закон Джоуля – Ленца

Расчёт электрических цепей постоянного тока основан на использовании закона Ома. Для участка однородной цепи (на котором не действуют сторонние силы) закон Ома выражает связь между током в цепи I, напряжением на концах участка U и сопротивлением R:

.

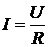Для неразветвлённой замкнутой цепи, содержащей источник тока с электродвижущей силой e и внутренним сопротивлением r, закон Ома имеет вид

.

А как найти силу тока в участке неоднородной цепи, между концами которого существует некоторая разность потенциалов и внутри которого имеются скачки потенциалов, например, включен гальванический элемент или аккумулятор?

Рассмотрим для простоты участок неоднородной цепи, состоящий из двух последовательно соединённых различных проводников A и B, например медного и цинкового (рис. 1). Между различными проводниками имеется скачок потенциала, который не зависит от тока и существует даже в его отсутствие. Этот скачок потенциала носит название внутренней контактной разности потенциалов. Его возникновение обусловлено тем, что число свободных электронов в единице объёма – концентрация электронного газа – различно в разных металлах. При соприкосновении таких металлов происходит диффузия электронов через контакт из того металла, где концентрация выше, в тот, где концентрация ниже. В результате между проводниками возникает разность потенциалов, величина которой определяется тем, что в установившемся динамическом равновесии диффузионный поток электронов уравновешивается встречным потоком, создаваемым возникшем в контактном слое электрическим полем. Величина скачка зависит от рода металлов и температуры. Подчеркнём, что каждый металл остаётся эквипотенциальным, а скачок потенциала и связанное с ним электрическое поле имеются только в месте контакта.

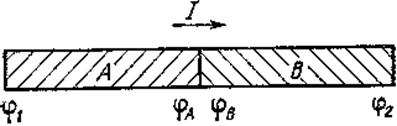
Рис. 1. Участок неоднородной цепи

Подсоединим теперь внешние концы проводников A и B к источнику постоянного напряжения. Обозначим потенциал левого конца проводника A через j₁, а потенциал правого конца проводника B через j₂ (рис. 1). Потенциалы металлов A и B в месте контакта обозначим через j _A и j _B. Так как теперь в проводниках идёт ток, то, разумеется, j₁ ¹ j _A и j₂ ¹ j _B. Мы пока не знаем, как записать закон Ома для всего рассматриваемого участка цепи, но зато можем написать его для каждого из однородных участков A и B. Так как проводники соединены последовательно, то через них протекает один и тот же ток I. Предположим, что ток идёт слева направо, как показано на рис. 1. Тогда

j₁ – j _A = IR_A,

j _B – j₂ = IR_B,

где R_A и R_B – сопротивления участков A и B. Сложим почленно эти уравнения и перегруппируем слагаемые в левой части следующим образом:

(j₁ – j₂) + (j _B – j _A)= I (R_A + R_B).

Сумма R_A + R_B есть полное сопротивление R рассматриваемого участка:

R_A + R_B = R.

Разность потенциалов j₁ – j₂ представляет собой приложенное напряжение U:

j₁ – j₂ = U.

Разность j _B ‑ j _A есть скачок потенциала в месте контакта металлов, который, как уже отмечалось, не зависит от протекающего тока и определяется только природой металлов и температурой. Значение скачка j _B ‑ j _A обозначим через e:

j _B – j _A = e.

Тогда соотношение (j₁ – j₂) + (j _B – j _A)= I (R_A + R_B) можно переписать в виде

.

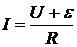Это и есть закон Ома для участка неоднородной цепи. Отметим, что под напряжением U на рассматриваемом участке понимается разность j₁ – j₂, где j₁ – потенциал той точки, от которой течёт ток, j₂ – потенциал точки, к которой течёт ток. Скачок потенциала в месте контакта e определён как j _B – j _A, т.е. знак e определяется тем, повышает или понижает скачок значение потенциала в цепи в направлении протекания тока: если повышает, то e > 0, если понижает, то e < 0. Но ведь при рассуждениях мы выбрали направление тока слева направо наугад! А если на самом деле он течёт в противоположную сторону? Предположив, что ток идёт справа налево, и, повторяя буквально все выкладки, мы получим значение тока, отличающееся только знаком. Это означает, что, приступая к анализу участка неоднородной цепи, мы можем вообще не задумываться о том, в какую сторону идёт ток на самом деле, а задавать ему направление произвольно. Выбрав направление тока, мы определяем его величину по формуле 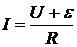, строго соблюдая сформулированное выше правило знаков для U и e. Если в результате ток окажется положительным, то он действительно течёт в заданном нами направлении. Если же получится отрицательное значение, то в действительности ток идёт в противоположную сторону, а величина его, разумеется, найдена правильно. Ниже мы подробно рассмотрим примеры использования закона Ома для участка неоднородной цепи, иллюстрирующие сформулированное правило знаков.

Скачок потенциала на границе двух металлов мы обозначили той же буквой e, что и электродвижущую силу. Это не случайно. Скачок потенциала возникает в результате диффузии электронов, т.е. сил неэлектростатического происхождения (не кулоновских), обусловленных хаотическим движением электронов. Такие силы неэлектростатического происхождения называют сторонними. Отношение работы A сторонних сил по перемещению положительного заряда q вдоль некоторого участка цепи к величине этого заряда носит название электродвижущей силы e на данном участке:

.

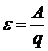В рассмотренном случае работа сил, вызывающих диффузию, при перемещении заряда против электрического поля в контакте определяется величиной скачка потенциала. Поэтому это действительно электродвижущая сила в обычном смысле этого слова. Но, конечно, такой контакт двух различных металлов в обычных условиях не может служить источником тока. Легко убедиться, что в замкнутой цепи из разных металлов, все участки которой поддерживаются при одной и той же температуре, сумма всех скачков потенциала равна нулю и ток в цепи отсутствует. Если поддерживать контакты при разных температурах, то сумма скачков не равна нулю и представляет собой термоэлектродвижущую силу.

Закон Ома для участка неоднородной цепи 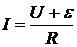справедлив не только в случае контактной разности потенциалов, но и для сторонних сил любой природы. Неоднородность участка может быть обусловлена наличием гальванического элемента, аккумулятора, генератора постоянного тока и т.д. Если рассматриваемый участок содержит несколько ЭДС, то в формуле 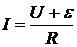под e нужно понимать алгебраическую сумму всех ЭДС, причём знак каждой из них определяется в соответствии со сформулированным правилом. В этом случае R представляет собой полное сопротивление участка.

Закон Ома в форме 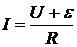содержит в качестве частных случаев формулы 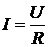и . Для однородного участка цепи e = 0 и 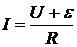превращается в 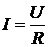. Для неразветвлённой замкнутой цепи U = 0 и формула 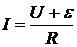переходит в .

При прохождении тока в цепи электрическое поле совершает работу, которую обычно называют работой тока. Величина работы постоянного тока I за время t на участке цепи, на концах которого поддерживается напряжение U, определяется соотношением

A = IUt.

Прохождение тока через проводник, обладающий сопротивлением, всегда сопровождается выделением тепла. Количество выделившегося за время t тепла определяется законом Джоуля – Ленца:

Q = I ² Rt.

В случае однородного участка, когда 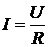, формулы A = IUt и Q = I ² Rt совпадают, т.е. количество выделяющегося тепла равно работе тока, и работу тока можно выразить любым из трёх эквивалентных способов:

.

В неоднородных участках цепи, где ток определяется формулой 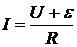, выделяющееся тепло не равно работе тока:

Q ¹ A.

Это означает, что протекание тока в таком участке сопровождается не только выделением тепла, но и другими процессами, связанными с превращением энергии.

В качестве примера энергетических превращений в неоднородной цепи рассмотрим зарядку аккумулятора. Не вдаваясь в детали происходящих в аккумуляторе процессов, легко сообразить, что при зарядке все химические процессы внутри него идут «вспять», и, следовательно, ток идёт в направлении, противоположном току при разрядке, когда аккумулятор является источником питания для внешней цепи. Поэтому аккумулятор включается в цепь так, как показано на рис. 2, а ток в цепи идёт в направлении, указанном стрелкой.

Рис. 2. Схема включения аккумулятора на зарядку

Так как ЭДС аккумулятора (сумма скачков потенциала внутри него) понижает потенциал в цепи в направлении протекания тока, то, в соответствии с законом Ома для неоднородного участка 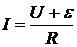, ток в цепи равен

.

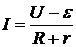В этой формуле r – внутреннее сопротивление аккумулятора, а сопротивление R включено в цепь для регулировки величины зарядного тока. Ток будет положительным и, следовательно, пойдёт в указанном направлении только при условии, что подаваемое напряжение U больше электродвижущей силы аккумулятора e:

U > e.

Только при выполнении этого условия и можно зарядить аккумулятор.

Работа, совершаемая зарядной станцией в единицу времени, т.е. работа тока в единицу времени на всём рассматриваемом участке, равна IU:

.

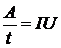На всех сопротивлениях, включая внутреннее сопротивление аккумулятора, в единицу времени выделяется джоулево тепло, равное I ²(R + r). Кроме зарядки аккумулятора и выделения тепла, других энергетических превращений в рассматриваемой цепи не происходит. Поэтому на основании закона сохранения энергии можно утверждать, что

IU = I ²(R + r) + P _зар,

где P _зар – мощность, идущая непосредственно на зарядку аккумулятора. Подставляя в IU = I ²(R + r) + P _зар выражение для силы тока 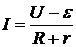, получим

.

Таким образом, при зарядке аккумулятор в единицу времени запасает энергию, равную Ie. Разумеется, этого результата можно было ожидать из элементарных соображений: ведь процессы в аккумуляторе считаются обратимыми, а при разрядке аккумулятор развивает мощность Ie.

Обратим внимание, что, считая известными выражения для полной работы тока (), для джоулева тепла (Q = I ²(R + r) t) и для работы зарядки аккумулятора (A _зар = P _зар t = eIt), можно с помощью закона сохранения энергии получить выражение 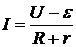для тока в цепи, т.е. закон Ома для данного случая. Для этого нужно просто подставить в IU = I ²(R + r) + P _зар выражение P _зар = Ie:

IU = I ²(R + r) + Ie,

.

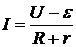Исследуем условия работы источника постоянного тока, замкнутого на внешнее сопротивление R (рис. 3): каким должно быть сопротивление нагрузки R для того, чтобы получить максимальную силу тока в цепи (I _max), максимальную полезную мощность (P _{п max}), максимальный коэффициент полезного действия (h _max)?

Дано: 1) I = I max; 2) P п =P п max; 3) h = h max.	Решение. 1) Ток в цепи определяется законом Ома: 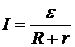. 2) Полная мощность P, развиваемая источником тока, равна
R –?

.

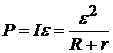Полезная мощность P _п, т.е. мощность, выделяющаяся на нагрузке, даётся соотношением

.

3) Коэффициент полезного действия h источника в этой цепи, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки:

.

Рис. 3. К исследованию условий работы источника тока

Исследуем полученные выражения. Полная мощность P (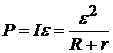) и ток в цепи I (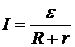) отличаются постоянным множителем e, поэтому их зависимость от сопротивления нагрузки R одинакова (кривая 1 на рис. 4). Максимальное значение этих величин (т.е. полной мощности и тока в цепи) (P _max и I _max) получается при R = 0, т.е. при коротком замыкании источника:

;

.

Как видно из формул и , при этом равны нулю полезная мощность P _п и коэффициент полезного действия h:

P _п = 0;

h = 0.

При R = r полная мощность и ток равны половине своего максимального значения:

;

;

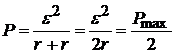коэффициент полезного действия h равен 0,5:

;

а полезная мощность достигает своего максимального значения, равного половине полной мощности P при этой нагрузке:

.

Докажем, что при R = r полезная мощность P _п достигает своего максимального значения: P _п = P _{п max}.

Первый способ

1. Найдём производную P _п по R:

.

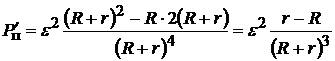2. Приравняем производную P _п по R к нулю:

,

,

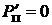R = r.

При переходе через точку R = r производная 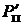меняет знак с «+» на «–». Значит, R = r – точка максимума.

Следовательно, при R = r полезная мощность P _п достигает своего максимального значения: P _п = P _{п max}.

Второй способ

Для того чтобы убедиться, что при равенстве сопротивления нагрузки R и внутреннего сопротивления источника тока r (R = r) полезная мощность P _п максимальна (P _п = P _max), преобразуем правую часть выражения 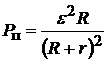следующим образом:

.

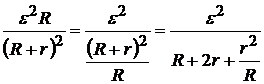Полезная мощность будет максимальной, когда знаменатель 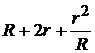минимален. Преобразуем знаменатель:

.

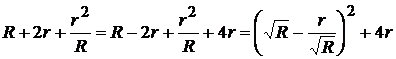Функция 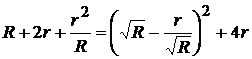достигает минимума тогда, когда , т.е. R = r.

При неограниченном увеличении сопротивления нагрузки (R ® ¥) как полная (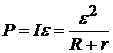) (кривая 1), так и полезная () мощность (кривая 2) стремятся к нулю:

P ® 0;

P _п ® 0;

а коэффициент полезного действия h () – к единице (кривая 3):

h ® 1.

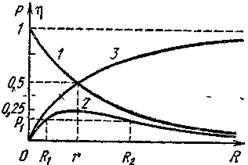
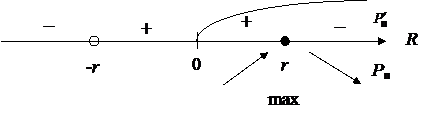
Рис. 4. Зависимость мощности и КПД источника тока от сопротивления нагрузки

Из рис. 4 видно, что требования получения максимального тока в цепи (I _max), максимальной полезной мощности (P _{п max}) и максимального КПД (h _max) противоречивы:

I = I _max при R = 0;

P _п = P _{п max} при R = r;

h = h _max при R ® ¥;

(P = P _max при R = 0).

Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника r, но при этом близки к нулю полезная мощность (P _п = 0) и КПД (h = 0): почти вся совершаемая источником тока работа идёт на выделение тепла на внутреннем сопротивлении r. Чтобы получить от данного источника тока максимальную полезную мощность (P _{п max}), следует взять нагрузку с сопротивлением R, равным внутреннему сопротивлению источника: R = r. Величина максимальной полезной мощности 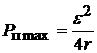, но коэффициент полезного действия при этом равен всего лишь 0,5: h = 0,5. Любую полезную мощность P ₁, меньшую максимальной, мы можем получить, как свидетельствует ход кривой 2, при двух значениях R ₁ и R ₂ сопротивления нагрузки. Практически для получения заданной полезной мощности следует выбирать нагрузку с большим сопротивлением R ₂, так как КПД при этом выше. Для получения КПД, близкого к единице, следует брать нагрузку с сопротивлением, много большим внутреннего сопротивления источника тока, но при этом выделяющаяся мощность P _п ® 0.

Не нашли, что искали? Воспользуйтесь поиском: