Цепи переменного тока. Векторные диаграммы. Резонанс

Физические процессы, происходящие в цепях синусоидального переменного тока, представляют собой вынужденные колебания, полный анализ которых сводится к решению дифференциальных уравнений с постоянными коэффициентами. Однако наиболее важный для практических применений установившийся режим таких колебаний, когда собственные колебания в цепи уже затухли, может быть строго исследован элементарными методами.

Прежде всего рассмотрим простейшие случаи, когда переменное напряжение U (t) = U ₀ cos w t подаётся на нагрузку, представляющую собой либо обычное омическое сопротивление R, либо ёмкость C, либо индуктивность L.

В случае активного сопротивления R ток в цепи I определяется соотношением

, ,

откуда видно, что в такой цепи не происходит сдвига по фазе между напряжением и током.

В цепи, содержащей только ёмкость C, ток проще всего найти, воспользовавшись тем, что его величина определяется скоростью изменения заряда конденсатора:

.

Так как

q = CU,

а ёмкость конденсатора постоянна:

C = const,

то для тока получаем

.

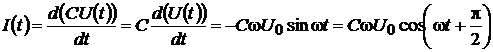Таким образом, ток в цепи имеет синусоидальный характер и опережает по фазе напряжение на :

.

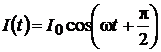Связи между амплитудными значениями подаваемого напряжения U ₀ и тока в цепи I ₀ можно, как видно из , придать вид закона Ома, если ввести понятие зависящего от частоты w емкостного сопротивления R_C:

, .

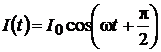(Из и следует, что

I ₀ = C w U ₀.

А так как

,

то

,

откуда

.)

Полученный результат можно наглядно проиллюстрировать с помощью графиков зависимости напряжения и тока от времени (рис. 8). В те моменты времени, когда подаваемое напряжение достигает экстремальных значений, заряд на конденсаторе не меняется и, следовательно, ток в цепи обращается в нуль. В точках, где напряжение обращается в нуль, величина его меняется наиболее быстро и, следовательно, ток достигает экстремальных значений. Итак, физическая причина сдвига по фазе очевидна, величина сдвига равна , а направление сдвига (опережение или отставание по фазе) легко установить, рассматривая, например, первую четверть периода изменения напряжения: напряжение убывает, т.е. конденсатор разряжается, несмотря на то, что ток увеличивается по абсолютной величине. Это возможно, только если напряжение и ток имеют противоположные знаки, т.е. график тока действительно имеет вид, изображённый на рис. 8.

Рис. 8. Напряжение и ток в конденсаторе

Случай, когда синусоидальное напряжение подаётся на индуктивность L, проще всего проанализировать, сравнивая выражения

, .

Первая формула представляет собой выражение для тока в только что рассмотренной цепи, содержащей ёмкость C. Второе соотношение выражает тот факт, что поданное на индуктивность L синусоидальное напряжение U в каждый момент времени компенсирует возникающую в катушке электродвижущую силу самоиндукции

.

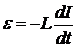Анализ соотношения привёл к формуле . Следовательно, формула такого же типа будет получена при анализе соотношения . Она получается из заменой I «U, C ® L:

.

Из соотношения следует, что ток I опережает напряжение U на ; аналогично из следует, что в такой цепи напряжение опережает ток на . Задаваемой величиной является подаваемое напряжение U (t) = U ₀ cos w t, поэтому для тока I получаем

.

(Или из выражаем I:

.

Так как U (t) = U ₀ cos w t, то

.

При t = 0 ток I = 0, т.е. I (0) = 0. Значит,

,

откуда

const = 0.

Следовательно,

.)

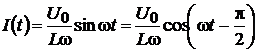Как и раньше, связи между амплитудными значениями тока и напряжения можно придать вид закона Ома, если, воспользовавшись , ввести индуктивное сопротивление R_L:

, R_L = w L.

(Из и следует, что

U ₀ = L w I ₀.

А так как

,

то

,

откуда

R_L = w L.)

Полученный результат также можно проиллюстрировать с помощью графиков (рис. 9). На верхнем графике показана зависимость тока от времени. На втором графике изображена ЭДС самоиндукции. (Так как 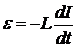, а , то

.)

Положение экстремумов и сдвиг этого графика относительно графика тока легко определить с помощью закона электромагнитной индукции и правила Ленца: 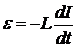. Действительно, ЭДС индукции обращается в нуль в точках экстремума тока и достигает экстремальных значений в те моменты, когда ток меняется наиболее быстро. В каждый момент полярность ЭДС самоиндукции такова, чтобы препятствовать изменению тока, ‑ этим сразу устанавливается направление сдвига по фазе между током и ЭДС самоиндукции. И, наконец, приложенное напряжение изменяется в противофазе с ЭДС самоиндукции (нижний график на рис. 9).

Рис. 9. Ток, ЭДС самоиндукции и напряжение на индуктивности

Рассмотрение этих простейших цепей показывает, что, за исключением случая активного сопротивления R, невозможно описать закон Ома для цепей переменного тока, определяющий мгновенное значение тока I (t) в виде отношения приложенного напряжения к сопротивлению соответствующего участка, вследствие того, что между током и напряжением существует сдвиг по фазе. Как мы видели, закон Ома справедлив только для амплитудных значений тока и напряжения.

Теперь рассмотрим последовательную цепь переменного тока, содержащую активное сопротивление R, ёмкость C и индуктивность L (рис. 10). К этой цепи приложено напряжение U (t) = U ₀ cos w t.

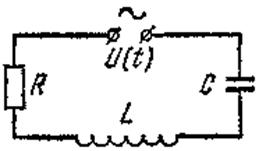
Рис. 10. Последовательная цепь RLC

В последовательной цепи переменного тока сила тока I в каждый момент времени во всех участках цепи одинакова, а сумма мгновенных значений напряжений на сопротивлении R, ёмкости C и индуктивности L равна значению приложенного напряжения в тот же момент времени:

U = U_R + U_C + U_L.

Воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по гармоническому закону величины можно представить как проекцию вектора на некоторое заранее выбранное направление, причём сам вектор равномерно вращается в плоскости с частотой w, а его длина равна амплитудному значению исследуемой величины. С помощью такого представления исследуемой схеме можно сопоставить векторную диаграмму, изображённую на рис. 11, а. Каждой величине: току I, напряжениям на сопротивлении R, ёмкости C и индуктивности L – сопоставляются векторы, длина которых равна амплитудному значению соответствующей величины. Вся система векторов вращается как целое с угловой скоростью w вокруг оси, перпендикулярной плоскости рисунка. Мгновенные значения величин I, U_R, U_L и U_C получаются проектированием соответствующих векторов на заранее выбранное направление NN. Поскольку, как мы видели, ток в цепи находится в фазе с напряжением U_R, отстаёт на от напряжения на индуктивности и опережает на напряжение на ёмкости U_C, то при выбранном направлении вращения вектор U _{0 L} опережает векторы I ₀ и U _{0 R} на , которые в свою очередь опережают на вектор U _{0 C}.

Как теперь найти вектор U ₀, изображающий приложенное напряжение U? Для этого нужно просто найти сумму векторов U _{0 R}, U _{0 L} и U _{0 C}, так как проекция результирующего вектора, которая и определяет мгновенное значение приложенного напряжения U, равна сумме проекций составляющих векторов, представляющих собой мгновенные значения напряжений U_R, U_L и U_C, в полном соответствии с равенством U = U_R + U_C + U_L (рис. 11, б). Из этого рисунка видно, что

, .

Используя связь между амплитудным значением тока I ₀ и амплитудными значениями напряжений на отдельных элементах цепи:

U _{0 R} = I ₀ R, , U _{0 L} = I ₀w L,

с помощью , получаем

,

откуда

, .

Итак, если приложенное напряжение U (t) = U ₀ cos w t, то ток в цепи I (t) = I ₀ cos (w t – j), где I ₀ и j определяются формулами и . Ток в цепи, как и напряжение, меняется по синусоидальному закону, но между током и напряжением существует сдвиг по фазе, равный j.

С помощью векторной диаграммы на рис. 11 б теперь легко написать выражения для мгновенных значений напряжений на отдельных элементах схемы:

U_R = U _{0 R} cos (w t – j) = I ₀ R cos (w t – j),

,

.

Рис. 11. а) Векторная диаграмма для последовательной цепи RLC (рис. 10). б) К определению связи между приложенным напряжением и током в цепи

Выясним, что покажет вольтметр, если его подключить к какому-либо из элементов схемы. Если вольтметр проградуирован так, что он показывает действующее значение напряжения, то его показания будут в раз меньше амплитудного значения напряжения на том элементе схемы, к которому он подключен. Произведя измерения напряжений на всех элементах схемы по отдельности, можно убедиться, что сумма этих напряжений всегда больше действующего значения подаваемого на схему напряжения. Более того, напряжение на любом из реактивных сопротивлений может быть гораздо больше подаваемого напряжения. Напряжение же на активном сопротивлении никогда не бывает больше подаваемого напряжения.

Если при измерении напряжений на реактивных элементах напряжения окажутся равными друг другу, то это значит, что равны реактивные сопротивления:

.

Такую ситуацию называют резонансом напряжений в цепи переменного тока. При этом напряжение на активном сопротивлении равно приложенному внешнему напряжению. Сопротивление всей последовательной цепи при резонансе напряжений становится чисто активным и равным R. Сдвиг фаз между приложенным напряжением и током в этом случае отсутствует.

Перейдём теперь к рассмотрению цепи переменного тока, содержащей параллельно соединённые активное сопротивление R, индуктивность L и ёмкость C (рис. 12), на которую подаётся переменное синусоидальное напряжение U (t) = U ₀ cos w t. Как и в случае последовательного соединения элементов, эту цепь удобно исследовать с помощью векторных диаграмм. Напряжение на всех параллельно соединённых элементах одинаково и равно приложенному напряжению U (t). Мгновенное значение тока в неразветвлённой части цепи I (t) равно алгебраической сумме токов в параллельных участках:

I = I_R + I_C + I_L.

Поскольку ток через сопротивление R находится в фазе с приложенным напряжением (I (t) = I ₀ cos w t), ток в ветви, содержащей ёмкость, опережает напряжение на (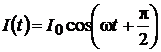), а ток через индуктивность отстаёт от напряжения на (), то векторная диаграмма, соответствующая этой цепи, имеет вид, изображённый на рис. 13. Учитывая связь между амплитудными значениями токов в различных элементах и амплитудным значением приложенного напряжения:

,

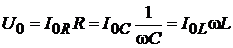с помощью векторной диаграммы на рис. 13 нетрудно получить следующие выражения для амплитуды тока в неразветвлённой части цепи и для сдвига по фазе между приложенным напряжением и этим током:

,

.

Таким образом, ток в неразветвлённой части цепи равен I (t) = I ₀ cos (w t – j), где I ₀ и j определяются формулам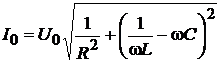и и . Векторная диаграмма даёт также возможность написать выражения для мгновенных значений тока в отдельных ветвях цепи:

,

,

.

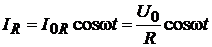Рис. 12. Параллельное соединение R, L и C

Рис. 13. Векторная диаграмма для параллельной цепи RLC (рис. 12)

При равенстве емкостного и индуктивного сопротивлений, т.е. при

,

сдвиг фаз между током в неразветвлённой части цепи и напряжением обращается в нуль. Токи I_C и I_L при этом равны по величине, и так как они находятся в противофазе, то ток в неразветвлённой части становится равным току I_R через активное сопротивление. Заметим, что токи I_L и I_C в отдельных ветвях цепи могут значительно превосходить ток в подводящих проводах. Такая ситуация носит название резонанса токов. При этом происходит обмен энергией между электрическим и магнитным полями, сосредоточенными в ёмкости и индуктивности, а источник питания только компенсирует потери энергии за счёт выделения джоулева тепла на сопротивлении R. Если R ® ¥, то энергетические потери в такой идеализированной схеме вообще отсутствуют, и ток в подводящих проводах равен нулю, хотя в контуре, состоящем из L и C, ток может быть очень большим. В этом случае на резонансной частоте

полное сопротивление контура неограниченно возрастает.

Резонанс токов, наряду с резонансом напряжений, широко используется в технике. В качестве примера рассмотрим работу простейшего резонансного усилителя, в анодной цепи которого имеется колебательный контур, настраиваемый на частоту сигнала, который требуется усилить (рис. 14). Для резонансной частоты (точнее, для узкой полосы частот) контур представляет собой большое сопротивление, и резонансный усилитель действует таким же образом, как и обычный усилитель на сопротивлениях, причём роль анодного сопротивления играет колебательный контур. Для частот, заметно отличающихся от резонансной, контур представляет собой короткое замыкание анодной цепи, и поэтому усиления сигнала не происходит.

Рис. 14. Принципиальная схема резонансного усилителя

Другим важным примером использования резонанса токов является индукционная печь, в которой нагревание металлов производится вихревыми токами. Параллельно нагревающей катушке присоединяют конденсатор и подбирают его ёмкость так, чтобы получить на частоте питающего генератора резонанс токов. Тогда через подводящие провода и генератор пойдёт сравнительно небольшой ток, который может быть во много раз меньше тока в колебательном контуре, образованном конденсатором и нагревающей катушкой.

Законы

Закон Ома. Зависимость силы тока от напряжения носит название закона Ома. Согласно закону Ома для участка цепи сила тока прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R:

.

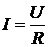Правило Ленца. При увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки. Ведь вектор индукции этого поля направлен против вектора индукции , порождающего электрический ток. Если же магнитный поток через катушку ослабевает, то индукционный ток создаёт магнитное поле с индукцией , увеличивающей магнитный поток через витки катушки.

В этом состоит существо общего правила определения направления индукционного тока, которое применимо во всех случаях. Это правило было установлено русским физиком Ленцем.

Согласно правилу Ленца возникающий в замкнутом контуре индукционный ток противодействует тому изменению магнитного потока, которым вызван данный ток. Или при всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему индукционный ток.

Рис. 15

Применять правило Ленца для нахождения направления индукционного тока I_i в контуре надо так:

1. Установить направление линий магнитной индукции внешнего магнитного поля.

2. Выяснить, увеличивается ли поток магнитной индукции этого поля через площадь контура (DФ > 0) или уменьшается (DФ < 0).

3. Установить направление линий магнитной индукции магнитного поля индукционного тока I_i. Эти линии должны быть согласно правилу Ленца направлены противоположно линиям при DФ > 0 и иметь одинаковое с ними направление при DФ < 0.

4. Зная направление линий магнитной индукции , найти направление индукционного тока I_i, пользуясь правилом буравчика.

Электромагнитной индукцией называется возникновение электродвижущей силы в проводнике при его перемещении в магнитном поле либо в замкнутом проводящем контуре вследствие его движения в магнитном поле или изменения самого поля. Эта электродвижущая сила e_инд. называется электродвижущей силой электромагнитной индукции. Под её влиянием в замкнутом проводнике возникает электрический ток, называемый индукционным током.

Закон электромагнитной индукции (закон Фарадея ‑ Максвелла): ЭДС e_инд. электромагнитной индукции в контуре пропорциональна и противоположна по знаку скорости изменения магнитного потока Ф_m сквозь поверхность, натянутую на этот контур, т.е.

.

При этом несущественно, чем именно вызвано изменение магнитного потока – деформацией контура, его перемещением в магнитном поле или изменением самого поля с течением времени. Направление обхода контура при вычислении e_инд. и направление нормали при вычислении Ф_m должны быть согласованы по правилу правого винта: из конца вектора обход контура должен быть виден происходящим против часовой стрелки.

Правило буравчика. В магнитном поле прямолинейного проводника с током магнитная стрелка устанавливается по касательной к окружности, плоскость которой (окружности) перпендикулярна проводу, а центр её лежит на оси провода. Направление вектора магнитной индукции устанавливают с помощью правила буравчика. Правило буравчика состоит в следующем: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращение ручки буравчика совпадает с направлением вектора магнитной индукции.

Рис. 16

Расчёт сложных (разветвлённых) цепей состоит в отыскании токов в различных участках таких цепей.

Узлом называется точка разветвлённой цепи, в которой сходится более двух проводников.

Первое правило Кирхгофа. Первое правило Кирхгофа (правило узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю:

,

где n – число проводников, сходящихся в узле,

I_i – ток в узле.

Положительными считаются токи, подходящие к узлу, отрицательными – токи, отходящие от узла.

Второе правило Кирхгофа. Второе правило Кирхгофа (правило контуров): в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре:

,

где n – число отдельных участков, на которые контур разбивается узлами. Для применения второго правила Кирхгофа выбирается определённое направление обхода контура (по часовой стрелке или против неё). Положительными считаются токи, направления которых совпадают с направлением обхода контура. ЭДС источников электрической энергии считаются положительными, если они создают токи, направления которых совпадают с направлением обхода контура.

Электрическим током называют упорядоченное (направленное) движение заряженных частиц. Электрический ток возникает при упорядоченном перемещении свободных электронов или ионов.

Электрический ток имеет определённое направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению движения частиц[1].

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура. На рисунке 17 положительным (произвольно) считают направление обхода против часовой стрелки. Если при обходе цепи переходят от отрицательного полюса источника к положительному, то ЭДС e > 0. Сторонние силы внутри источника совершают при этом положительную работу. Если же при обходе цепи переходят от положительного полюса источника к отрицательному, ЭДС будет отрицательной. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 17, при обходе контура против часовой стрелки

e = e ₁ + e ₂ + e ₃ = ï e ₁ï – ï e ₂ï + ï e ₃ï.

Рис. 17

Если e > 0, то согласно сила тока I > 0, т.е. направление тока совпадает с направлением обхода контура. При e < 0, наоборот, направление тока противоположно направлению обхода контура.

a   Функция

– w t – 2p

– w t – p

– w t

– w t + p

– w t + 2p

w t – 2p

w t – p

w t + p

w t + 2p

sin a

– sin w t

cos w t

sin w t

– cos w t

– sin w t

cos w t

sin w t

– cos w t

– sin w t

sin w t

cos w t

– sin w t

– cos w t

cos w t

– sin w t

– cos w t

sin w t

cos a

cos w t

sin w t

– cos w t

– sin w t

cos w t

sin w t

– cos w t

– sin w t

cos w t

cos w t

– sin w t

– cos w t

sin w t

– sin w t

– cos w t

sin w t

cos w t

tg a

– tg w t

ctg w t

– tg w t

ctg w t

– tg w t

ctg w t

– tg w t

ctg w t

– tg w t

tg w t

– ctg w t

tg w t

– ctg w t

– ctg w t

tg w t

– ctg w t

tg w t

ctg a

– ctg w t

tg w t

– ctg w t

tg w t

– ctg w t

tg w t

– ctg w t

tg w t

– ctg w t

ctg w t

– tg w t

ctg w t

– tg w t

– tg w t

ctg w t

– tg w t

ctg w t

a   Функция	– 2p = – 3600		– p = – 1800				p = 1800		2p = 3600
sin a				– 1				– 1
cos a			– 1				– 1
tg a		–		–		–		–
ctg a	–		–		–		–		–

[1] Такой выбор направления тока не очень удачен, так как в большинстве случаев ток представляет собой движение электронов – отрицательно заряженных частиц. Выбор направления тока был сделан в то время, когда о свободных электронах в металлах ещё ничего не знали.

Не нашли, что искали? Воспользуйтесь поиском: