Порядок обработки результатов при прямых многократных измерениях

1. Истинное значение измеряемой величины вычисляется как сред­нее арифметическое всех n измерений:

. (1.14)

2. Определяется абсолютная погрешность каждого измерения:

Δ х₁ = | х _ист – х ₁|,

Δ х₂ = | х _ист – х ₂ |,

Δ х₃ = | х _ист – х ₃|,

Δ х_ш = | х _ист – х_i|. (1.15)

3. Рассчитывается среднее арифметическое абсолютных погрешностей каждого измерения:

. (1.16)

Следует иметь в виду, что данная формула справедлива только для малого количества измерений (n < 10).

4. Оценивается приборная погрешность.

5. Вычисляется результирующая абсолютная погрешность по формуле (1.10).

6. По формуле (1.12) находится относительная погрешность.

7. Результат измерений записывается в виде (1.13).

Например, необходимо обработать результаты измерений температуры физического тела (измерения проводились термометром, точность кото­рого 1⁰С). Было проведено три измерения, при которых получены следующие значения: t₁ = 24,5°С; t₂ = 25°С; t ₃ = 25,5°С.

1. Находим среднее арифметическое:

(t) ₌ .

2. Определяем отклонения результатов измерения от его среднего значения:

t₁ = [ 25–24,5] = 0,5,

t₂ = [25–25 ] = 0,

t ₃ = [25–25,5] = 0,5.

3. Рассчитываем среднюю абсолютную погрешность:

.

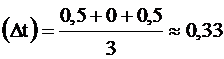4. Приборная погрешность, равна 1⁰С.

5. Вычисляем результирующую абсолютную погрешность:

.

6. Находим относительную погрешность:

.

7. Результат измерений записываем в виде:

t = (25±1,05)°С.

Не нашли, что искали? Воспользуйтесь поиском: