СЛУЧАЙНЫЕ ПОГРЕШНОСТИ

При наличии случайных погрешностей результат отдельного наблюдения х_k измеряемой величины х является случайной величиной. В этом случае результаты наблюдений х₁, х₂, …, х_n одной и той же величины х различны. В качестве результата измерения принимается среднее арифметическое значение результатов наблюдений:

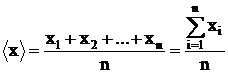. (1.1)

Предел результата измерения при n®¥ называется математическим ожиданием m:

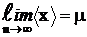. (1.2)

Случайную величину х, являющуюся результатом отдельного наблюдения, можно задать с помощью функции распределения f(х) (функции плотности вероятности):

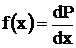или 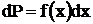, (1.3)

где dP - вероятность попадания случайной величины в интервал
(х, х+dx) шириной dx.

Если случайная величина зависит от большого количества неконтролируемых изменяющихся причин, то она подчиняется нормальному распределению или распределению Гаусса. Функция распределения Гаусса для случайной величины х с математическим ожиданием m описывается формулой:

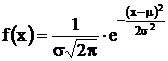, (1.4)

где 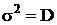- дисперсия распределения. Величина называется стандартным или среднеквадратичным отклонением. График функции распределения Гаусса показан на рис.1.

Математическое ожидание m определяет положение оси симметрии кривой распределения, а величина s характеризует разброс х относительно m.

С учетом формулы (1.3) вероятность Р попадания результата наблюдения х в интервал (х₁, х₂) равна

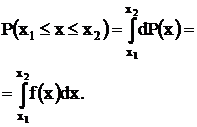
Рассмотрим интервал, в центре которого находится математическое ожидание m, а полуширина равна

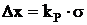, (1.5)

где 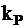- некоторое число. Вероятность Р наблюдения случайной величины х, подчиняющейся нормальному распределению, в таком интервале определяется формулой:

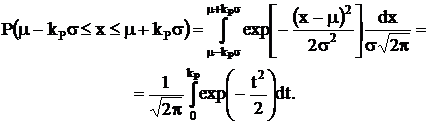(1.6)

Вычисление интеграла в формуле (1.6) показывает, что при
k_P = 1,0 вероятность Р = 0,68, т.е. 68% результатов наблюдений лежат внутри интервала (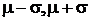). Соответственно, при k_P = 2,0 получим Р = 0,95, а при k_P = 3,0 вероятность Р = 0,997.

Пусть наличие случайных погрешностей приводит к тому, что результат наблюдения х измеряемой величины подчиняется нормальному распределению. Параметры m и s этого распределения экспериментатор не знает. В процессе измерения получают n результатов наблюдений: х₁, х₂, …, х_n, т.е. получают некоторую выборку значений х из генеральной совокупности допустимых значений. Определяя результат измерения 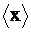по формуле (1.1), находят выборочную оценку величины m. Выборочную оценку дисперсии нормального распределения результатов наблюдений получают по формуле

, (1.7)

где S(х) - выборочная оценка стандартного отклонения результата наблюдения; n - число наблюдений.

Если результат отдельного наблюдения х является случайной величиной, подчиняющейся нормальному распределению с дисперсией D(х), то результат измерения , определяемый по формуле (1.1), также подчиняется нормальному распределению с дисперсией 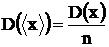. Соответственно, выборочная оценка стандартного отклонения результата измерения равна

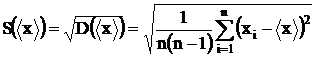. (1.8)

Теоретически показано, что для каждой вероятности Р (меры доверия) можно построить такой доверительный интервал (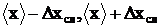), что математическое ожидание m случайной величины х окажется внутри этого интервала с вероятностью Р. Полуширина такого доверительного интервала определяется формулой:

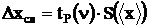, (1.9)

где S() находим по формуле (1.8), а 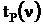- коэффициент Стьюдента, величина которого зависит от вероятности Р и числа степеней свободы n (см. таблицу Приложения). Число степеней свободы n связано с числом наблюдений n формулой: 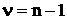. Можно показать, что в формуле (1.5) коэффициент

. (1.10)

При наличии только случайных погрешностей запись результата измерения: .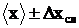

Не нашли, что искали? Воспользуйтесь поиском: