Оценить диаметр ее молекулы.

Молярная масса воды:

Если молекулы в жидкости упакованы плотно и каждая из них вписывается в куб объемом V₁ с ребром d, то .

Объем одной молекулы: ,где: V_m одного моля, N_A - число Авогадро.

Объем одного моля жидкости: , где: М- ее молярная масса, - плотность.

Диаметр молекулы:

Вычисляя, имеем:

Относительная молекулярная масса алюминия Mr=27. Определить его основные молекулярные характеристики.

1.Молярная масса алюминия: M=Mr^.10^-3 M = 27 ^.10^-3

2. Количество вещества, содержащееся в одном килограмме алюминия:

3. Количество вещества, содержащееся в 1 м³

алюминия:

4. Масса 5 моль алюминия: .

5. Число частиц, содержащееся в 1 кг алюминия:

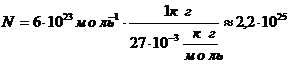
6. Число частиц, содержащееся в 1м³

алюминия:

7. Порядок величины радиуса атома алюминия, считая, что атомы имеют форму шара и

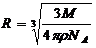
расположены вплотную:

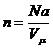
1. Концентрация

молекул:

или:

; .

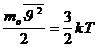2.Среднеквадратичная скорость молекул:

;

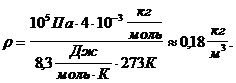
3. Плотность:

Мы не знаем, одинаковой ли остается температура воздуха в пузырьке. Если она одинакова, то процесс всплытия описывается уравнением pV=const. Если изменяется, то уравнением pV/T=const.

Оценим, большую ли ошибку мы допускаем, если пренебрегаем изменением температуры.

Предположим, что мы имеем максимально неблагоприятный результат.Пусть стоит очень жаркая погода и температура воды на поверхности водоема достигает +25 ⁰С(298 К). На дне температура не может быть ниже +4 ⁰С (277К), так как этой температуре соответствует максимальная плотность воды. Таким образом, разность температур составляет 21К. По отношению к начальной температуре, эта величина составляет % %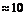.Вряд ли мы встретим такой водоем, перепад температур между поверхностью и дном которого равен названной величине. К тому же, пузырек всплывает достаточно быстро и вряд ли за время всплытия он успеет полностью прогреться. Таким образом, реальная ошибка будет существенно меньшей и мы вполне можем пренебречь изменением температуры воздуха в пузырьке и воспользоваться для описания процесса законом Бойля-Мариотта: p₁V₁=p₂V₂, где: p₁ - давление воздуха в пузырьке на глубине h (p₁ = p_атм. + rgh), p₂ - давление воздуха в пузырьке вблизи поверхности. p₂ = p_атм.

(p_{атм +} rgh)V =p_атм 2V; ;

В перевернутом вверх дном стакане закупорен воздух. В задаче утверждается, что стакан начинает тонуть только на некоторой глубине. По всей видимости, если его отпустить на глубине меньшей некоторой критической глубины, он всплывет (предполагается, что стакан расположен строго вертикально и не опрокидывается).

Уровень, находясь выше которого стакан всплывает, а ниже которого тонет, характеризуется равенством сил, приложенных к стакану с разных сторон.

Силами, действующими на стакан в вертикальном направлении, являются сила тяжести, направленная вниз, и выталкивающая сила, направленная вверх.

Выталкивающая сила связана с плотностью жидкости, в которую помещен стакан, и объемом вытесненной им жидкости.

Сила тяжести, действующая на стакан, прямо пропорциональна его массе.

Из контекста задачи вытекает, что по мере погружения стакана, сила, направленная вверх, уменьшается. Уменьшение выталкивающей силы может происходить только за счет уменьшения объема вытесненной жидкости, так как жидкости практически несжимаемы и плотность воды у поверхности и на некоторой глубине одинакова.

Уменьшение объема вытесненной жидкости может происходить за счет сжатия воздуха в стакане, которое, в свою очередь, может идти за счет увеличения давления. Изменение температуры, по мере погружения стакана, можно не учитывать, если нас не интересует слишком высокая точность результата. Соответствующее обоснование приведено в предыдущем примере.

Связь давления газа и его объема при постоянной температуре выражается законом Бойля-Мариотта.

Давление жидкости действительно увеличивается с глубиной и передается во все стороны, в том числе и вверх, одинаково.

Гидростатическое давление прямо пропорционально плотности жидкости и ее высоте (глубине погружения).

Записав в качестве исходного уравнения уравнение, характеризующее состояние равновесия стакана, последовательно подставив в него найденные в ходе анализа задачи выражения и решив полученное уравнение относительно искомой глубины, приходим к тому, что для получения численного ответа нам необходимо знать значения плотности воды, атмосферного давления, массы стакана, его объема и ускорения свободного падения.

Все проведенные рассуждения можно отобразить следующим образом:

Поскольку в тексте задачи нет никаких данных, зададим их самостоятельно.

Дано:

Плотность воды r=10³ кг/м³.

Атмосферное давление 10⁵ Па.

Объем стакана 200 мл = 2 00^.10^-3 л = 2 ^. 10 ^-4 м³.

Масса стакана 50 г = 5^. 10^-2 кг.

Ускорение свободного падения g = 10 м/с².

Численное решение:

Задача о подъеме воздушного шара так же, как и задача о тонущем стакане, может быть отнесена к классу статических задач.

Шар начнет подниматься так же, как и стакан тонуть, как только нарушится равенство сил, приложенных к этим телам и направленных вверх и вниз. На шар, так же, как и на стакан, действуют сила тяжести, направленная вниз и выталкивающая сила, направленная вверх.

Выталкивающая сила связана с плотностью холодного воздуха, окружающего шар. Эта плотность может быть найдена из уравнения Менделеева-Клапейрона.

Сила тяжести прямо пропорциональна массе шара. Масса шара, в свою очередь, складывается из массы оболочки и массы горячего воздуха, находящегося внутри него. Масса горячего воздуха также может быть найдена из уравнения Менделеева-Клапейрона.

Схематически рассуждения могут быть отображены следующим образом:

Из уравнения можно выразить искомую величину, оценить возможные значения необходимых для получения численного решения задачи величин, подставить эти величины в полученное уравнение и найти ответ в численном виде.

1. Выразите массу газа в СИ.

2. Чему равна относительная молекулярная масса данного газа?

3. Чему равна молярная масса данного газа (в СИ)?

4. Чему равно количество вещества, содержащегося в сосуде?

5. Сколько молекул газа находится в сосуде?

6. Чему равна масса одной молекулы данного газа?

7. Назовите процессы на участках 1-2, 2-3, 3-1.

8. Определите объем газа в точках 1,2, 3, 4 в мл, л, м³.

9. Определите температуру газа в точках 1,2, 3, 4 в ⁰С, К.

10. Определите давление газа в точках 1, 2, 3, 4 в мм. рт. ст., атм, Па.

11. Изобразите данный процесс на графике зависимости давления от абсолютной температуры.

12. Изобразите данный процесс на графике зависимости давления от объема.

Указания к решению:

1. См. условие.

2. Относительная молекулярная масса элемента определяется с помощью таблицы Менделеева.

3. M=M_r ·10^-3 кг/моль.

4. 5. 6.

7. p =const - изобарический; V =const-изохорический; T =const - изотермический.

8. 1 м³ = 10³ л; 1 л = 10³ мл. 9. T = t + 273. 10. 1 атм. = 10⁵ Па = 760 мм.рт. ст.

8-10. Можно воспользоваться уравнением Менделеева-Клапейрона, либо газовыми законами Бойля-Мариотта, Гей-Люссака, Шарля.

Ответы к задаче

m = 0,2 кг
Mr = 4
M = 4 · 10 -3 кг/моль
n = 50 моль
N = 3 · 1025
m =6,7 · 10 -27 кг
1 - 2 - изобарический
2 - 3 - изохорический
3 - 1 - изотермический
№	мл	л	м3
	2 · 10 5		0,2
	7 · 10 5		0,7
	7 · 10 5		0,7
	4 · 10 5		0,4
№	0С	К
№	мм.рт.ст.	атм	Па
	7,6 · 10 3		106
	7,6 · 10 3		106
	2,28 · 10 3		0,3 · 106
	3,8 · 10 3		0,5 · 106

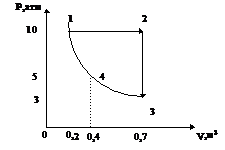
Не нашли, что искали? Воспользуйтесь поиском: