Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме

Скалярное произведение векторов E и d S называется потоком вектора напряженности d Ф_Е через площадку d S (рис. 1.2.): d Ф_E = Е∙ d S = Е∙ d S cosa= Е_n d S, где a – угол между векторами n и Е; Е_n = Е cosa – проекция вектора Е на нормаль n к площадке d S.

Если плоская поверхность S перпендикулярна силовым линиям однородного электрического поля, то поток напряженности через нее

Ф_Е = Е∙S.

Для неоднородных полей поток напряженности поля через всю поверхность представится суммой элементарных потоков:

.

Единицей измерения потока вектора напряженности электростатического поля является вольт-метр (В·м). Поток вектора напряженности электростатического поля зарядов q в вакууме (e = 1) через сферическую поверхности радиусом R, охватывающую этот заряд, находящийся в ее центре (рис. 1.3):

,

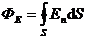Во всех точках сферы | E| одинакова, и силовые линии перпендикулярны поверхности. Следовательно, . Площадь поверхности сферы равна 4p R ². Отсюда

.

На рис. 1.4 представлена произвольная замкнутая поверхность, охватывающая заряд q >0. Некоторые линии напряженности то выходят из поверхности, то входят в нее. Нечетное число пересечений сводится к одному: линии, выходящие из поверхности – положительные, а линии, входящие – отрицательные. Если замкнутая поверхность не охватывает заряд, то Ф_Е = 0. Если замкнутая поверхность охватывает несколько зарядов, то

Не нашли, что искали? Воспользуйтесь поиском: