Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность ра-

вен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрическую постоянную e₀.

Эта формулировка представляет собой теорему К. Гаусса.

Применяя теорему Гаусса, можно определить напряженности полей, создаваемых заряженными телами различной формы:

1) напряженность поля равномерной бесконечной плоскости

;

2) напряженность поля двух бесконечных равномерно заряженных плоскостей ;

3) напряженность поля заряженной сферической поверхности

,

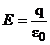где величина называется поверхностной плотностью заряда.

1.4. Работа сил электростатического поля при перемещении заряда. Циркуляция вектора напряженности электростатического поля. Потенциальная энергия и потенциал электростатического поля

При перемещении заряда в электростатическом поле действующие на заряд кулоновские силы совершают работу. Пусть точечный заряд q ₀ > 0 перемещается в поле другого точечного заряда q > 0 из точки С в точку В вдоль произвольной траектории (рис. 1.5). При элементарном перемещении заряда d l эта сила совершает работу d A:

d A = F ·d l = F d l cosa,

где a – угол между векторами F и d l; d l cosa = d r – проекция вектора d l на направление силы F. Таким образом,

d A = F d r, .

Полная работа по перемещению заряда q ₀ из точки С в точку В определяется интегралом

где r ₁ и r ₂ – расстояния от заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении заряда q ₀ в поле заряда q, не зависит от формы траектории движения, а зависит только от начального и конечного положений заряда. Следовательно, электростатическое поле точечного заряда – потенциальное, а действующие в нем силы – консервативные.

Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е. Так как d A = F d l и F = E q ₀, то d A = q ₀ E d l. Отсюда получаем . Если заряд q ₀ является единичным положительным точечным, то получим

,

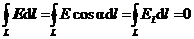где E_l = E cosa – проекция вектора Е на направление элементарного перемещения d l. Интеграл называется циркуляцией вектора напряженности. Таким обра­зом, циркуляция вектора напряженности электростатического поля вдоль лю­бого замкнутого контура равна нулю. Это заключение справедливо для потенциаль­ного поля.

Работа в таком поле совершается за счет убыли потенциальной энергии:

A = – Δ W _п = W _п1 – W _п2.

Используя формулу работы силы электростатического поля по перемещению заря­да, получим

= = W _п1 – W _п2.

Анализируя полученное выражение, можно сделать вывод, что потенциальная энергия точечного заряда q ₀ в поле заряда q равна

.

Если поле создано системой зарядов q ₁, q ₂,..., q_n, то потенциальная энергия за­ряда q ₀:

.

Потенциальная энергия заряда q ₀ зависит от его величины. Однако отношение потенциальной энергии заряда q ₀ к его величине является постоянным для данной точки поля и может служить энергетической характеристикой дан­ной точки поля. Отношение называется потенциалом электростатичес­кого поля j:

.

Потенциал j– скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда, поме­щенного в данную точку поля.

Ранее было записано A = W _п1 – W _п2. Так как W _п1 = φ ₁ q ₀ и
W _п2 = φ ₂ q ₀, то A = q ₀(φ ₁ – φ ₂) и Δ φ = (φ ₁ – φ ₂) = .

Разность потенциалов Δ φ двух точек поля численно равна работе сил поля по перемещению единичного положительного заряда из точки 1 в точку 2.

Если заряд q ₀ перемещать из какой-либо точки поля в бесконечность, то r ₂ ® ¥, W _п2 = 0 и φ ₂ = 0. Тогда работа A _∞ по перемещению заряда q₀ в бесконечность:

A _∞ = q ₀ φ ₁, φ ₁ = .

Потенциал точки поля численно равен работе, совершаемой электрическими силами при перемещении единичного положи-тельного заряда из данной точки поля в бесконечность.

Потенциал точки поля системы зарядов q ₁, q ₂,..., q_n равен алгебраической сумме потенциалов полей всех этих зарядов:

.

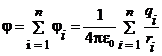Единицей потенциала является вольт (В).

Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, потенциал всех точек которых одинаков. Если поле создано точечным зарядом, эквипотенциальные поверхности в данном случае – концентрические сферы, а линии напряженности перпендикулярны эквипотенциальным поверхностям (рис 1.6).

Не нашли, что искали? Воспользуйтесь поиском: