Распределение молекул по скоростям

Так как тепловое движение — хаотическое (беспорядочное), то скорости молекул имеют всевозможные случайные значения, различающиеся по величине и направлению (имеют всевозможные проекции, например, на ось х). До сих пор удавалось обходиться среднеквадратичной скоростью, главное свойство которой заключалось в том, что кинетическая энергия, пропорциональная среднему квадрату скорости á V 2ñ, сама прямо пропорциональна температуре Т. Для одной молекулы (массой т 0) двухатомного газа

(3.3)

где

(3.4)

Напомним, эта величина называется постоянной Больцмана.

Отсюда среднеквадратичная скорость молекулярного движения

(3.5)

прямо пропорциональна корню квадратному из температуры и обратно пропорциональна корню квадратному из молярной массы газа.

Если необходимо характеризовать скорости молекул (или другие их характеристики) более подробно, то нужно использовать методы статистики. Статистика — наука о качественных характеристиках массовых объектов (здесь молекул), имеющих случайные свойства. Основные методы статистики — это методы теории вероятностей. В основе слова «статистика» (statistics) можно увидеть корень «state» (штат, государство). Массовые явления нужно анализировать, чтобы понимать процессы в государстве. Существует огромная область физики и химии — статистическая физика. Здесь будут рассмотрены лишь отдельные элементы этой науки.

Итак, удобно молекулы разделить на группы с близкими скоростями — скоростями, лежащими в интервале от V до dV. Всего молекул в газе N, а молекул со скоростями в заданном интервале будет dN. Так как молекул «много», то и N — велико, и dN — велико. Поэтому удобно характеризовать тепловое движение «долей» молекул, имеющих скорости от V до Δ V. Такая доля dN / N — это отношение числа молекул, имеющих скорость, близкую к требуемой, к общему числу молекул.

Очевидно, что чем больше интервал скоростей dV ≈ Δ V, в который входят молекулы из dN ≈ Δ N, тем и само число молекул со скоростями в этом интервале dN тоже больше. Короче, доля Δ N / N прямо пропорциональна Δ V — интервалу скоростей. Коэффициент пропорциональности между долей молекул газа dN / N, имеющих скорость, близкую к какой-то (любой, но одной) скорости V и интервалом скоростей Δ V, в котором скорости считаются «близкими», зависит уже только от самой этой избранной скорости, обозначается F (V) и называется функцией распределения.

(3.6)

Конечно, функцией распределения можно характеризовать не только величины (модули) скоростей, но и, например, проекции скорости на любую ось (назовем ее осью x):

(3.7)

Функции распределения различных величин — характеристик множества молекул, несколько различаются, но в главном они одинаковы. Мало молекул с «крайними» характеристиками. Мало очень «быстрых» и мало очень «медленных». Вот с какими-то «средними» значениями скорости (модуля скорости) молекул будет «много» (рис. 3.2).

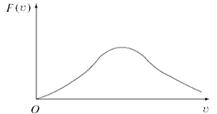
Рис. 3.2. Распределение молекул по скоростям (по величинам скоростей)

Также и молекул, быстро летящих вдоль оси x как в положительном, так и в отрицательном направлении, будет немного, а молекул с малыми проекциями скоростей (т. е. с большими проекциями на другие оси) гораздо больше (рис. 3.3).

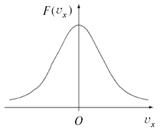
Рис. 3.3. Распределение молекул по проекциям скорости

Такой вид функций распределения подтверждается на опыте.

Рассмотрим физический смысл функции распределения F (V). Пусть газ содержит N молекул. Найдем число молекул dN, скорости которых имеют значение от V до V + dV. Очевидно, площадь, закрашенная на рис. 3.4, есть вероятность обнаружения таких молекул, т. е. их относительное число dN / N.

Рис. 3.4. Физический смысл функции распределения Максвелла: закрашенная площадь — доля молекул со скоростями от V до V + dV

Поскольку величина закрашенной площади равна F (V) dV,то

(3.8)

Таким образом, число молекул со скоростями в интервале (V, V + dV) равно

dN = NF (V) dV. (3.9)

Вероятность

Доля молекул, имеющих скорости, лежащие в интервале от V до V + dV, выражаемая ранее величиной dN / N, в математике называется вероятностью.

Действительно, вероятностью какого-либо события (исхода) называется отношение числа благоприятных исходов к общему числу испытаний (исходов). В «молекулярной науке» общее число исходов испытаний — это, очевидно, общее число молекул N. Благоприятным исходом считается тот, когда молекула имеет скорость, лежащую в интервале от V до V + dV.

Такое совпадение позволяет применять к поиску функции распределения F (V), по определению связанной с вероятностью dN / N соотношением F (V) dV = dN / N, методы, развитые и глубоко исследованные в области математики, называемой теорией вероятностей.

Рассмотрим самые азы теории вероятностей на очевидном примере с подбрасыванием монеты и угадыванием — предсказанием: «Что выпадает: орел или решка?» Что такое «решка»? Не понятно. Но в примере ясно — это другая (не орел) сторона монеты. Пусть благоприятным исходом считается выпадение орла — одно событие. Всего исходов — два. Вероятность благоприятного исхода — 1/2. Если делать два бросания, то вероятность, что оба раза выпадет орел (сокращенно «О»), будет 1/4. Действительно, это одно из ОО, ОI, IО, II — четырех возможных исходов (исход решки обозначим I). А если подбросить трижды, то какова вероятность, что все три раза будет орел? 1/6? Нет. Надо выбирать из ООО, ОIО, IОО, ПО, ООI, ОII, IОI, III. Это 1/8. А два орла? Какова вероятность, что дважды выпадет О? Очевидно, 3/8 (второй, третий и пятый исходы). Три раза из восьми возможных. Также легко подсчитать, что вероятность одного О при тех же восьми возможных будет 3/8. Наконец, вероятность, что орел ни разу «не покажет свой клюв», будет 1/8 (исход III).

Попробуем на основе этих примеров сделать общие заключения. Во-первых, видим, что вероятности одинаковых, независимых друг от друга событий (повторное выпадение орла), перемножаются. Во-вторых, обратим внимание на сумму полученных вероятностей. При одном бросании 1/2 + 1/2 = 1, при трех бросаниях 1/8 + 3/8 + 3/8 + 1/8 = 1. То есть сумма вероятностей всех исходов равна единице.

Из этих двух положений можно сделать некоторые заключения о функции распределения. Пусть вероятность, что молекула имеет проекцию скорости от Vx до Vx + dVx, будет F (Vx) dVx. Так как все оси равноправны, то вероятность, что три проекции лежат, каждая соответственно в интервале от Vx до Vx + dVx, от Vу до Vу + dVу и от Vz до Vz + dVz, будет произведение F (Vx) ⋅ F (Vу) ⋅ F (Vz) ⋅ dVx ⋅ dVу ⋅ dVz. Но тремя проекциями определяется величина скорости (модуль) 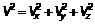и направление.

Тогда

(3.10)

где F (V) dV — вероятность, что скорость имеет величину, лежащую от V до V + dV, F (θ, φ) d θ d φ — вероятность, что скорость направлена под углами от θ до θ + d θ и от φ до φ + d φ.

Формула (3.10) и выражает положение о перемножении вероятностей, но в применении к вероятностям, связанным со скоростью молекулы. Применим теперь положение о нормировке, так называется сформулированное ранее правило о том, что сумма вероятностей всех исходов равна единице. Это правило называется условие нормировки. При малых интервалах величин скоростей, для которых вычисляется вероятность (а дифференциалы соответствуют «бесконечно малым» интервалам), сумма заменяется интегралом и, например,

(3.11)

где пределы интегрирования показывают всю область изменения переменных. Формула (3.11) представляет собой математическое выражение условия нормировки в различных случаях.

Величина вектора (рис. 3.5) V — положительна, изменяется от 0 до ¥. Проекция может быть и отрицательна (когда она направлена против оси). Углы можно все охватить (рис. 3.6), если пол-окружности (с θ от 0 до π) повернуть на полный оборот от φ = 0 до φ = 2π.

Рис. 3.5. Модуль и направление скорости

Рис. 3.6. Область изменения углов 0 < φ < 2π, 0 < θ < π

Вернемся теперь к примерам о бросании монеты и посмотрим внимательно на числители дробей, которые отражают количество (не вероятность — долю, а число — количество) благоприятных исходов — то количество исходов, когда выполняется наперед заданное условие о числе выпадений орла.

Если внимательно присмотреться, то числа благоприятных исходов совпадают с коэффициентами многочлена, возникающего при возведении двучлена в степень. Например, (p + q)3 = р 3 + 3 р 2 q + 3 pq 2 + q 3, а числа выпадения орла соответственно 1, 3, 3, 1 (при отсутствии выпадений, одном выпадении, двух выпадениях и трех выпадениях) в трех бросаниях. Оказывается, этот результат вполне общий.

Количество благоприятных исходов совпадает с биномиальными коэффициентами. Вспомним, что двучлен по латыни — бином. Итак:

(3.12)

где

(3.13)

— число сочетаний из k элементов по m элементов. Обозначение же факториала — знакомое, именно k! = 1 ⋅ 2 ⋅ 3 ⋅... ⋅ k — произведение всех натуральных чисел до k.

Более того, если рассматривать р как вероятность выпадения благоприятного исхода в одном испытании (бросании), a q = 1 – р — вероятность, что благоприятный исход не выпадет, то каждое слагаемое в биномиальном разложении (3.12) — вероятность выхода благоприятного исхода равно m раз в k испытаниях. Это легко проверить, например при р = 1/2 и q = 1 – 1/2 = 1/2, взяв k = 3.

Интересно, что график (рис. 3.7) зависимости числа сочетаний от числа благоприятных исходов m имеет такой же «колоколообразный» вид, как и график распределения молекул по проекции скорости, приведенный ранее (см. рис. 3.3).

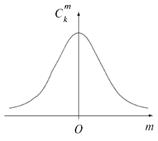
Рис. 3.7. График зависимости числа сочетаний из k элементов по m при больших значениях k

Итак, вероятность, что событие наступит ровно m раз при k независимых испытаниях (формула Бернулли):

(3.14)

Однако вычислять по этой формуле при сколько-нибудь значительном числе испытаний очень трудно (громоздко). Примерно двести лет тому назад Пьер-Симон Лаплас установил, что если число испытаний K велико, то эту вероятность можно приближенно подсчитать по формуле

(3.15)

где

(3.16)

Постоянные А и В определяются соответственно из условия нормировки и из условия, что наибольшая вероятность по точной и по приближенной формуле будет в одной и той же точке. Так как молекул очень много, то для вероятностей в статистической физике формулу Лапласа используют как точную.

Подведем итог нашего, пусть поверхностного, но нужного изучения основ теории вероятностей.

1. Вероятность появления хоть одного из несовместимых (невозможных) одновременно событий равна сумме вероятностей этих событий. Сумма всех вероятностей (интеграл) равна единице.

2. Вероятность появления нескольких событий, независимых от других, равна произведению вероятностей этих событий.

3. Формула Бернулли и Лапласа. Вероятность того, что в k независимых испытаниях, в каждом из которых вероятность появления событий равна р, событие наступит ровно m раз безразлично в какой последовательности, равна:

(3.17)

Здесь коэффициент появляется из условия нормировки, из того, что сумма всех вероятностей равна единице. При вычислении соответствующего интеграла использовано, что

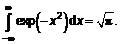(3.18)

Заметим в заключение, что теория вероятностей — красивая наука, облегчающая понимание явлений жизни и природы.

Не нашли, что искали? Воспользуйтесь поиском: