
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Адиабатический процесс
В уравнение состояния газа входят три термодинамических параметра: p,V,T. Первое начало термодинамики также оперирует тремя величинами dQ,dU, dА. Выше мы рассмотрели простейшие процессы, при которых один из термодинамических параметров остается постоянным. При этом, поскольку внутренняя энергия идеального газа определяется только температурой (U=m/mCuT), изотермический процесс является в то же время процессом постоянной внутренней энергии (dU=0). Аналогично этому можно сказать, что изохорный процесс (V=const) является процессом без совершения работы (dA=0). Таким образом, из простейших процессов, описываемых названными шестью величинами, мы не рассмотрели только процесс, в котором dQ=0.
 |
р
V
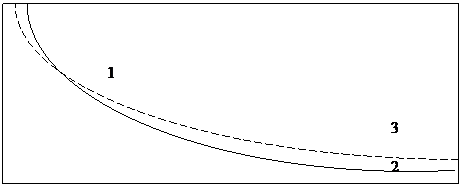
Рис. 2.4. График адиабатического процесса (пунктирная линия – изотерма)
Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой. В таком процессе Q=0, причем не только суммарное количество теплоты, полученное термодинамической системой, равно нулю, но и в каждом элементарном процессе выполняется условие dQ=0.
При этом процессе температура изменяется, несмотря на отсутствие теплопередачи. При адиабатном процессе теплоемкость газа, в соответствии с определением (2.3), равна нулю. Примером такого процесса может быть рассмотренный выше процесс сжатия или расширения газа в цилиндре под поршнем при условии, что стенки цилиндра и поршень имеют идеальную тепловую изоляцию. Данный процесс изображен в координатах {р,V} линией 1 -2 (рис.2.2), которая называется адиабатой. Поскольку при адиабатном процессе Q=0, первое начало термодинамики имеет вид:
DU+Aад=0
откуда
Aад=-DU (2.18)
Таким образом, в адиабатическом процессе работа, совершается газом против внешних сил только за счет уменьшения внутренней энергии газа. Поэтому при адиабатическом расширении температура газа уменьшается, а при адиабатическом сжатии - увеличивается. В результате этого адиабата в плоскости {р, V} проходит круче, чем изотерма (кривая 1-3 на рис.2.4). Эффект адиабатического изменения температуры широко используется в технике, например при сжижении газов.
В дифференциальной форме первое начало термодинамики для адиабатического процесса имеет вид (dQ=0):
dU+p×dV=0. (2.19)
Заменяя в (2.19) dU выражением (2.9), и выразив р из уравнения состояния идеального газа, получим:
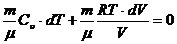 .
.
Разделив левую и правую часть этого выражения на m × СuT/m, получим:
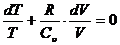 . (2.20)
. (2.20)
Для идеального газа Сu - постоянная величина, поэтому легко проинтегрировать равенство (2.20) и получить:
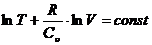 , или
, или 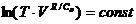 .
.
Логарифм какой-либо величины имеет постоянное значение, если под знаком логарифма также стоит постоянная величина, поэтому
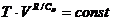 . (2.21)
. (2.21)
Это соотношение дает связь термодинамических параметров при адиабатическом процессе.
Безразмерная величина g=CР/Cu называется показателем адиабаты и определяется числом степеней свободы молекулы газа. Подставив значения CР и Cu из выражений (2.10) и (2.15), получим:
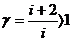 . (2.22)
. (2.22)
Через величину g удобно выразить показатель степени в уравнении (2.21). Действительно, из уравнения Майера (2.14) можно получить: R= CР- Cu в результате показатель R/ Cu можно преобразовать:
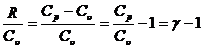 .
.
Подставив это выражение в формулу (2.21), запишем ее компактнее:
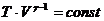 . (2.23)
. (2.23)
Из этого выражения следует, что T=const/V g-1, а поскольку согласно (2.22) g-1>0, температура уменьшается при адиабатическом расширении и, наоборот, увеличивается при сжатии. Этот вывод мы уже сделали раньше, исходя из первого начала термодинамики, но выражение (2.23) позволяет вычислить изменение температуры количественно. Например, если в начальном состоянии объем V1 и температура $T1 известны, а также известен конечный объем V2, то можно записать уравнение (2.21) для начального и конечного состояний:
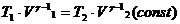 .
.
Из этого равенства найдем:
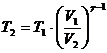 .
.
Характер изменения давления при адиабатическом процессе также можно найти, исходя из (2.23), если заменить в нем температуру, воспользовавшись уравнением Клайперона - Менделеева (T=pVμ/mR). В результате получим:
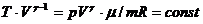 .
.
Поскольку m, μ, R являются постоянными для данной массы газа, полученное выражение можно записать в виде:
p.Vγ=const. (2.24)
Это соотношение называется уравнением адиабаты Пуассона.
Работа при адиабатическом расширении газа равна площади под кривой процесса 1-2 (см. рис.2.2). Если известны начальная и конечная температуры процесса, то нет необходимости вычислять эту площадь - достаточно воспользоваться формулой (2.18) и выражением для внутренней энергии идеального газа. Это приведет нас к соотношению:
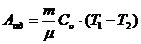 . (2.25)
. (2.25)
Не нашли, что искали? Воспользуйтесь поиском: