
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Термодинамические циклы. Цикл Карно
Циклом, как указывалось ранее, называется такой процесс, в результате которого термодинамическая система возвращается в исходное состояние. Циклы или круговые процессы используются во всех тепловых машинах: двигателях внутреннего сгорания, газотурбинных установках, холодильниках и т.п. Изучение циклов является одной из основных задач термодинамики.
 |
 p a
p a
 |
 1 2
1 2
b
 V
V
C D
 Рис. 2.5. Схема прямого цикла тепловой машины
Рис. 2.5. Схема прямого цикла тепловой машины
Рассмотрим произвольный цикл 1-а-2-b-1, изображенный на рис. 2.5. Его можно разбить на два процесса: 1-а-2 - процесс расширения и 2-b-1 - процесс сжатия. На участке 1-а-2 газ получает извне количество теплоты Q1 и в результате совершается работа и изменяется внутренняя энергия газа:
Q1=A1+(U2-U1). (*)
Работа A1 может быть найдена как площадь фигуры С1a2D.
На участке 2-б-1, наоборот, внешние силы совершают положительную работу A2 над газом, а работа газа – A2 при этом отрицательна. Для того, чтобы суммарная работа газа AΣ, численно равная площади фигуры, ограниченной кривой 1a2b1, при выбранном направлении цикла была положительна (AΣ=A1-A2>0), процесс сжатия должен происходить при меньшем давлении и температуре. Это означает, что в ходе процесса сжатия газ необходимо охлаждать, отводя от него тепло другому телу. Другими словами количество теплоты, полученное газом при сжатии –Q2 - величина отрицательная (Q2>0 - теплота, отданная газом). Таким образом, уравнение первого начала термодинамики для процесса 2-b-1 можно записать в виде:
-Q2=(U1-U2)-A2 / (**)
Из равенств (*) и (**) нетрудно получить
AΣ=A1-A2=Q1-Q2.
Это равенство выражает первое начало термодинамики для полного цикла. Оно показывает, во-первых, что работа совершается вследствие превышения теплоты Q1, полученной газом при расширении, над теплотой Q, отданной им при сжатии. Во-вторых, можно сделать вывод, что при циклическом процессе невозможно все полученное от нагревателя тепло превратить в работу - необходимо <<поделиться>> частью полученного тепла с другим телом, которое является холодильником.
КПД тепловой машины. Цикл с положительной работой газа называется прямым циклом и лежит в основе всех тепловых двигателей. В них рабочее вещество (газ или пар) получает от нагревателя некоторую теплоту, а отдает холодильнику теплоту Q2. Отношение
 . (2.26)
. (2.26)
показывает, какая доля полученной от нагревателя теплоты превращена в работу и носит название коэффициента полезного действия тепловой машины. Видим, что эта величина не может быть большей 1.
КПД холодильной машины. Если при круговом процессе газ, расширяясь, совершает работу, меньшую той работы, которую производят внешние силы при его сжатии, т.е. A1<A2, то такой цикл носит название обратного цикла. Он может происходить, когда расширение газа происходит при более низкой температуре, чем сжатие. Легко видеть, что обход прямого цикла на графике в координатах {p,V} всегда происходит по часовой стрелке, а обратного цикла - против часовой стрелки.
Обратные циклы используются в холодильных установках. В холодильных установках рабочее тело отбирает тепло Q2 у тела с более низкой температурой, вызывая его охлаждение, и отдает телу с более высокой температурой теплоту Q1 (по аналогии с прямым циклом Q2<Q1). Этот процесс требует совершения работы внешними силами, AΣ=A2 – A1. Первое начало термодинамики для обратного цикла запишется в виде:
Q2-Q1=A1-A2<0.
Поскольку цель холодильника - забрать тепло от охлаждаемого тела, а затраты при этом - совершаемая работа, эффективность холодильника можно характеризовать отношением Q2 к AΣ. Это отношение:
 . (2.27)
. (2.27)
может превышать 1 и называется холодильным коэффициентом.
Эффективность теплового насоса. Обратный цикл может использоваться также для обогрева. При этом теплота Q2 забирается из внешней среды и в обогреваемое помещение (при более высокой температуре) передается теплота Q1. Обогрев производится за счет внешней силы и все соотношения между величинами в точности совпадают с величинами для холодильника. Однако, поскольку цель в данном случае другая - обогреть помещение, то <<польза>> определяется количеством теплоты, переданным помещению т.е. величиной Q1, а затраты - по-прежнему состоят в совершении работы AΣ. Такое устройство называется тепловым насосом, а его эффективность определяется формулой:
Q1
 |
 p 2
p 2
 1
1
 | |||
 |
4 3
 |
V
Q2

 Рис. 2.6 Цикл Карно
Рис. 2.6 Цикл Карно

и всегда превышает единицу. В связи с этим заметим, что старый анекдот о том, что некоторые народности Крайнего Севера греются в холодильниках, имеет под собой научную основу! Правда бытовой холодильник в этом случае следует разместить камерой на улицу (с открытой дверцей), а теплообменником (задняя часть холодильника) - внутрь помещения.
Цикл Карно. В термодинамике особое место занимает цикл, рассмотренный французским инженером Сади Карно в 1824 году. Цикл состоит из четырех обратимых процессов для идеального газа (см. рис. 2.3.1). Подразумевается, что имеется нагреватель с температурой T1 и холодильник с температурой T2.
Участок 1-2 - изотерма с температурой Т1, участок 2-3 - адиабата, участок 3-4 - изотерма с температурой Т2, участок 4-1 - адиабата (две изотермы и две адиабаты). Подвод тепла к рабочему телу осуществляется на участке 1-2, а отвод тепла - на участке 3-4. Карно доказал, что КПД этого цикла максимальный по сравнению со всеми другими возможными рабочими циклами в диапазоне температур между Т1 и Т2, а также не зависит от рода рабочего тела. Действительно, на участке 1-2 тело получает от нагревателя теплоту, которая вся (без потерь) идет на выполнение работы (см. 2.17) A1-2:
 .
.
Значения объема V1 газа в точке 1 и V2 в момент окончания изотермического участка 1-2, как будет видно, не войдут в окончательное выражение для КПД.
Далее газ необходимо подготовить к стадии сжатия. Чтобы работа газа в цикле была положительной, необходимо понизить давление, охладив газ от температуры T1 до T2. Охлаждение осуществляется на участке 2-3 адиабатически. Этот процесс также оптимален, поскольку на этом участке не происходит потери тепловой энергии (δQ=0), а, кроме того, совершается дополнительная положительная работа A2-3 за счет уменьшения внутренней энергии газа (см. выражение 2.25)):
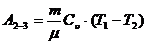 .
.
Таким образом, на стадии расширения газ совершил работу A1=A1-2+A2-3, получив теплоту Q1.
В процессе 3-4 изотермического сжатия газа от объема V3, который газ имел в конце адиабатического расширения, до некоторого объема V4 газ совершает работу A3-4, получив такое же по величине количество тепла Q3-4:
 .
.
Поскольку V4<V3, логарифм в этой формуле, а вместе с ним и величины Q3-4=A3-4 отрицательны, что означает не получение газом, а передачу тепла Q2=-Q3-4 холодильнику. Положительная работа также совершается внешними силами. Работа внешних сил на этом участке имеет наименьшее из возможных значение, поскольку газ все время имеет наименьшую температуру T2 (значит, и наименьшее давление).
Участок 4-1 необходим, чтобы вернуть газ в исходное состояние с температурой T1. Это нагревание в цикле Карно осуществляется также оптимальным образом - адиабатически (без затраты тепловой энергии). При этом работа A4--1<0, т.е. совершается над газом внешними силами.
Нетрудно убедиться, что A2-3=-A4-1 и работа газа на двух адиабатических участках компенсирует друг друга, так же как и изменение внутренней энергии (теплопередача на этих участках отсутствует). Поэтому основу цикла составляют два изотермических процесса, при первом из которых полученная теплота полностью превращается в работу, а второй происходит при наименьшей возможной температуре и давлении и соответствует наименьшей отрицательной работе газа и наименьшей теплоотдаче холодильнику. Эти доводы еще раз подчеркивают оптимальность цикла Карно.
Подставив величины Q1 и Q2 в общую формулу (2.26), вычислим КПД идеальной тепловой машины Карно:
 .
.
Найдем соотношения между объемами V1, V2, V3, V4. Напишем соотношение для адиабатного расширения газа от объема V2 до V3 и для адиабатического сжатия от объема V4 до V1 (см. формулу 2.21):
T1V2γ-1=T2V3γ-1,
T1V2γ-1=T2V4γ-1,
Поделим левую часть первого равенства на левую часть второго, а правую часть первого на правую часть второго (если делить два равных числа на равные числа, равенство сохранится):
 .
.
Это равенство можно упростить:
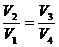
и с его помощью исключить V2/V1 в выражении для η. Это приведет к сокращению одинаковых логарифмических множителей. Окончательно получим:
 . (2.28)
. (2.28)
Этот вывод можно сформулировать так: термический КПД цикла Карно не зависит от природы рабочего тела и является только функцией температур нагревателя и холодильника. Это заключение получило название теоремы Карно.
Цикл Карно сыграл большую роль в развитии тепловых двигателей. Соотношение (2.28) показывает путь повышения КПД реальных двигателей: повышение температуры рабочего тела и снижение температуры холодильника. Одновременно можно утверждать, что в рамках заданных Т1, Т2 тот цикл будет иметь больший КПД, который ближе к циклу Карно.
Не нашли, что искали? Воспользуйтесь поиском: