Реальные газы. Уравнение Ван-Дер-Ваальса

Как отмечалось ранее, кинетическая теория идеального газа не учитывает сил взаимодействия молекул, сами же молекулы принимаются за точки. Такая модель соответствует достаточно разреженному газу, подчиняющемуся законам Бойля -Мариотта и Гей-Люссака.

Многочисленные опыты показали, что все газовые законы и, в частности, формула Клайперона - Менделеева носят приближенный характер. Чем сильнее сжат газ, тем заметнее его отклонение от газовых законов. Для того, чтобы можно было применить формулу Клайперона - Менделеева к реальным газам, очевидно, необходимо ввести в нее какие-то поправки. Одно из наиболее удачных уточнений этой формулы предложил в 1983 г. голландский физик Ван-дер-Ваальс.

Первое уточнение Ван-Дер-Ваальса касается объема самих молекул. В 1см³

газа при нормальных условиях содержится 2,7 10¹⁹ молекул. Принимая эффективный диаметр молекулы равным 3·10^-8см, определяем, что ее объем равен 1,2·10^-23см³. Находим, что объем всех молекул, находяхщихся в 1см³ газа при нормальных условиях, составляет около 3·10^-4см³. Однако при давлении 2500 атм объем самих молекул уже составит половину всего объема газа. Поэтому при высоких давлениях объем газа, занимаемый самими молекулами, необходимо учитывать.

Так как при сжатии газа уменьшается обратно пропорционально давлению не весь объем, а объем свободного пространства между молекулами, в формуле Клайперона - Менделеева вместо V следует ввести (V-b), где b – объем несжимаемой части газа. По вычислению Ван-Дер-Ваальса, b приблизительно равно учетверенному объему всех молекул. Поясним, как получается такой результат.

Действительно, центры молекул не смогут сблизиться больше, чем на расстояние, равное удвоенному эффективному радиусу (2r), т.е. проникнуть в пространство, соответствующее объему шара радиуса 2r (см. рис. 3.1). Объем такого шара равен , т.е. восьмикратному объему одной молекулы (V ₀= 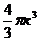) Следовательно, каждой из двух выделенных молекул соответствует объем несжимаемого пространства, равный учетверенному объему одной молекулы (4V₀).

Второе уточнение, введенное Ван-Дер-Ваальсом, касается давления газа. При разреженном состоянии газа силы сцепления между его молекулами ничтожно малы. Однако при сжатии газа промежутки между молекулами уменьшаются и силы их взаимодействия возрастают. Эти силы притяжения молекул друг к другу как бы помогают силам внешнего давления сжимать газ. Следовательно, в формулу Клайперона - Менделеева вместо внешнего давления p на газ необходимо ввести сумму внешнего и молекулярного давлений (p+p'), где p' – молекулярное давление. По вычислениям Ван-Дер-Ваальса, молекулярное давление обратно пропорционально квадрату объема газа, т.е.

,

Рис. 3.1. Объем пространства, недоступный центрам двух молекул в процессе их соударения (штрихованная линия)

где a – некоторый коэффициент пропорциональности, зависящий от природы газа.

Вводя указанные поправки, получим формулу

, (3.1)

называемую уравнением Ван-Дер-Ваальса и записанную для массы газа, равной одному молю (V_μ - объем одного моля газа). Значения коэффициентов a и b приводятся в справочниках также для 1 моля газа. Если масса m газа содержит ν=m/μ молей, то объем газа при прочих равных условиях увеличится в ν раз, т.е. V=νV_μ или V_μ=V/ν. Заменив молярный объем V_μ в формуле (3.1) при помощи полученного соотношения, получим уравнение Ван-дер-Ваальса для любой массы газа:

. (3.2)

Как мы уже отмечали, формула Клайперона - Менделеева хорошо описывает поведение достаточно разреженных газов. В табл. 3.1 приведены опытные данные для массы азота, занимающей при нормальных условиях объем, равный одному литру. Во втором столбце таблицы приведены значения произведения p V при разных давлениях и одной и той же температуре 0˚C. Это произведение согласно уравнению Клайперона - Менделеева должно оставаться постоянным, а отличие его от единицы указывает на отклонение поведения реального газа от идеального. Как видим, сколько-нибудь заметные расхождения с уравнением состояния идеального газа возникают при давлениях в сотни атмосфер и с ростом давления становятся существенными. В третьем разделе таблицы приведено при тех же условиях произведение подправленных давления и объема, которое должно оставаться постоянным при фиксированной температуре в соответствии с уравнением Ван-Дер-Ваальса. Как видим из таблицы, уравнение Ван-Дер-Ваальса гораздо лучше согласуется с экспериментом, чем уравнение Клайперона – Менделеева.

Т а б л и ц а 3.1

Р, атм	pV, a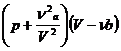тм · л	, атм · л
	1,000 0,994 1,048 1,390 2,069	1,000 1,000 1,009 1,014 0,893

Изотермы Эндрюса

Английский физик Эндрюс во второй половине прошлого века произвел ряд исследований свойств паров и построил экспериментальные изотермы. В толстостенный цилиндр под поршнем вводились пары углекислого CO₂, давление измерялось при помощи манометра.

При изотермическом уменьшении объема давление возрастало и на графике, соответствующем данному процессу (рис. 3.2), получался участок изотермы 1-2, приближающийся к гиперболе. Таким образом опыты Эндрюса подтвердили, что ненасыщающие пары подчиняются закону Бойля - Мариотта. Точка 2 соответствует объему V₂ и показывает состояние паров CO₂, при котором они насыщают пространство. При дальнейшем уменьшении объема в цилиндре часть паров переходит в жидкость, а давление оставшихся над жидкостью паров сохраняется при данной температуре неизменным. На графике получается участок 2-3, соответствующий одновременному существованию вещества в двух фазах (в двух агрегатных состояниях) - жидкой и газообразной.

Точка 3 соответствует объему V₃ и показывает такое состояние, когда пар полностью обращается в жидкость. Дальнейшее увеличение давления вызывает сжатие жидкости, а так как жидкости крайне слабо сжимаются, участок изотермы 3-4 представляет почти вертикальную линию, лишь незначительно приближающуюся к оси Y.

На рис. 3.3. показан ряд таких изотерм, соответствующих одной и той же массе CO₂, но построенных для разных температур. Чем выше температура, тем участок 2-3 короче, т.е. разность в объемах насыщающего пара (V₂) и полученной из него при полной конденсации жидкости (V₃) становится меньше.

При некоторой определенной температуре площадка 2-3 исчезает, на графике возникает точка перегиба K, которая носит название критической точки. Температура, при которой она получается, называется критической температурой (T_к), давление, соответствующее точке K - критическим давлением (p_к), а объем, занимаемый при этом молем газа - критическим объемом (V_к). При критической температуре ненасыщающий пар переходит в жидкое состояние, как бы минуя стадию насыщения. Для CO₂ критическая температура равна 31˚C, критическое давление около 73 атм.

p 4

2

0 V₂ V

Рис. 3.2. Изотерма паров СО₂, полученная в экспериментах Эндрюса

При температурах выше критической вещество может существовать только в газообразном состоянии и ни при каком давлении не обращается в жидкость.

Понятие о критической температуре впервые было введено в науку Д.И. Менделеевым 1861 г. Он отметил, что при повышении температуры силы взаимодействия между молекулами жидкости слабеют, коэффициент поверхностного натяжения жидкости уменьшается, а при некоторой температуре обращается в нуль. Эту температуру Менделеев назвал температурой абсолютного кипения.

р

р_к К

Жидкость+пар

0 V_k V

Рис. 3.3 Изотермы Эндрюса, соответствующие разным температурам

В табл. 3.2 приведены данные о критических температурах, давлениях и объемах для некоторых веществ.

Т а б л и ц а 3.2

Критические параметры некоторых веществ

Из этой таблицы, в частности, следует, что при температурах, больших 374˚C, вода не может существовать в жидком состоянии, какое бы давление мы на нее ни оказывали. Для получения сжиженных газов, их следует предварительно охлаждать до температуры ниже критической и установка должна создавать давление порядка p_к.

Не нашли, что искали? Воспользуйтесь поиском: