Взаимное расположение двух прямых в пространстве

Пусть прямые l ₁ и l ₂ заданы каноническими уравнениями

Обозначим = = 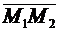(х ₂- x ₁, y ₂- у ₁, z ₂- z ₁), =(m ₁, n ₁, р),

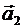= (m ₂, n ₂, р ₂).

1) если прямые совпадают, то все три вектора , , 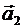коллинеарны.

2) если прямые параллельны и не совпадают, то вектора и 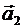коллинеарны, а вектор им не коллинеарен.

3) если пряже пересекаются, то никакие два из векторов , , 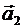не коллинеарны, и все три вектора компланарны.

4) ecли прямые скрещиваются, то векторы , , 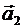некомпланарны.

Отметим, что условия параллельности и перпендикулярности, прямых l ₁ и l ₂ равносильны условиям коллинеарности и ортогональности их направляющих векторов и .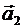

Следовательно,

- необходимое и достаточное условие параллельности двух прямых.

m ₁ m ₂ + n ₁ n ₂ + p ₁ p ₂ = 0

- необходимое и достаточное условие перпендикулярности двух прямых.

Если прямые l ₁ и l ₂ пересекаются, то величина угла φ между ними равно либо ( ^, 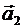) либо (- ^, 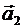). Следовательно,

Не нашли, что искали? Воспользуйтесь поиском: