Полярное уравнение эллипса, гиперболы, параболы

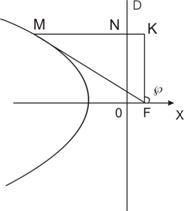
Выведем полярное уравнение для отличного от окружности эллипса, параболы или правой ветви гиперболы. Для этого совместим полюс полярной системы координат с левым фокусом эллипса (правым фокусом гиперболы) или единственным фокусом параболы, а полярную ось направим перпендикулярно директрисе d, соответствующей фокусу. Обозначим через F, р и ε соответственно фокус, фокальный параметр и эксцентриситет кривой. Пусть М — произвольная точка кривой, МF = r — полярный радиус точки М, φ — ее полярный угол. Тогда

─ полярное уравнение эллипса, отличного от окружности, параболы, правой ветви гиперболы.

Для левой ветви гиперболы

─ полярное уравнение левой ветви гиперболы.

Классификация кривых второго порядка (КВП)

Уравнение вида

a x²+ b ху+ с у²+ d x+ е у+ f =0, (1)

где a²+ b²+ c² ≠ 0, называется уравнением кривой второго порядка в прямоугольноу системе ккординат OXY. Преобразуем систему координат таким образом, чтобы уравнение (1) приняло наиболее простой вид.

1. Если в уравнении коэффициент b ≠ 0, то можно повернуть систему координат OXY на угол α такой, что в новой системе координат O’X’Y’ уравнение (1) не будет содержать член с произведением x’y’.

Действительно, согласно формулам поворота x = x’cosα – y’sinα, y = y’sinα + y’cosα.. Подставляя значения x и y в (1) легко подсчитать, что коэффициент при x’y’ примет вид

-2 a cosα sinα + b ²cos²α - b ²sin²α + 2 c sinα cosα.

Упрощая, получаем

- a sin2α + b cos2α + c sin2α = 0,

(a - c)sin2α = b cos2α, т.е.

,

Таким образом, в дальнейшем предполагаем, что уравнение КВП имеет вид

a x²+ b ху+ с у²+ d x+ е у+ f =0. (2)

2. Если в уравнении (2) а ≠ 0 и d ≠ 0, либо с ≠ 0 и е ≠ 0, то, осуществляя параллельный перенос системы координат ОХУ, получаем уравнение КВП, не содержащее член с х, соответственно у.

Действительно, пусть а ≠ 0, d ≠ 0. Выделим полный квадрат при переменной х в (2).

Применим формулы параллельного переноса

, ,

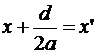Тогда уравнение примет вид

где . Если же с ≠ 0 и е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с у.

Итак можно считать, что КВП представляется одним из трёх видов уравнений:

ах ² + by ² + c = 0;

ах ² + by + c = 0;

аy ² + bх + c = 0.

Рассмотрим случаи:

1) с ≠ 0. Тогда

Если – (а/с) › 0 и – (b/c) › 0, то это уравнение эллипса.

Если – (a/c) ‹ 0 b – (b/c) ‹ 0, то получаем пустое множество точек на плоскости.

Если – (a/c) › 0 и – (b/c) ‹ 0, то уравнение гиперболы.

Аналогичным образом получам гиперболу вытянутую вдоль оси ОУ.

2) с = 0. Тогда ах ² + by ² = 0;

Если a и b – разных знаков, то всегда можно считать, что а › 0,

b ‹ 0.

Уравнение будет задавать две пересекающиеся прямые ax by = 0

Если же a и b одного знака, то уравнению удовлетворяет единственная точка О (0,0).

Вывод: любая кривая второго порядка является эллипсом, гиперболой, параболой, парой пересекающихся прямых, парой параллельных прямых, прямой, точкой или пустым множеством.

Укажем еще один способ классификации КВП.

Не нашли, что искали? Воспользуйтесь поиском: