Свойства определителей второго и третьего порядков

Будем рассматривать в дальнейшем только определители 3-го порядка. Для определителей 2-го порядка все свойства аналогичны.

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (операция транспонирования), т.е.

.

Действительно,

Δ=а₁b₂с₃+b₁с₂а₃+с₁а₂b₃—с₁b₂а₃—а₁с₂b₃—b₁a₂c₃. (*)

Δ'=а₁b₂с₃+c₁a₂b₃+b₁с₂а₃+с₁b₂а₃+а₁с₂b₃+b₁а₂с₃. (**)

Сравнивая равенства (*) и (**), получаем, что Δ=Δ'.

2. При перестановке 2-х строк (столбцов) местами определитель меняет знак на противоположный.

Доказательство проводится проверкой.

3. Если определитель имеет 2 одинаковые строки (столбца), то он равен нулю.

Действительно, при перестановке двух одинаковых строк, определитель Δ, очевидно не изменится. С другой стороны, по свойству 2 он изменит знак на противоположный. Следовательно, Δ= -Δ, т.е. Δ=О.

4. При умножении любой строки (столбца) определителя Δ на некоторое число λ, определитель умножается на это число, то есть, например,

.

Доказательство следует из того факта, что вычисляя определитель по правилу треугольника, получим, что каждое слагаемое содержит множитель . Вынося этот множитель за скобку, получим в скобке определитель Δ.

5. Если элементы 2-х строк (столбцов) определителя пропорциональны, то определитель равен нулю.

Пусть

Тогда по свойству 4,

т.е. по свойству 3 Δ₁ = 0.

6. Если элементы какой-либо строки (столбца) определителя представляют собой сумму 2-х слагаемых, то данный определитель равен сумме соответствующих определителей.

Пусть

Тогда

=

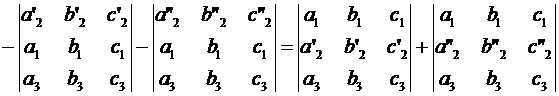
7. (Основное). Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое число, то величина определителя не изменится.

Итак, например,

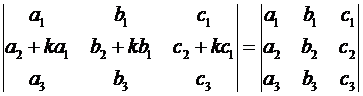
Доказательство следует из последовательного свойств 6 и 5.

8. (О разложении определителя по элементам i-й строки или j-го столбца).

Тогда минором элемента a_ij определителя Δ называется определитель M_ij полученный из данного, вычеркиванием строки и столбца, на пересечении которых стоит элемент а_ij.

Имеет место следующее равенство:

Δ=(-1)ⁱ⁺¹a_i1M_i1+(-1)ⁱ⁺²a_i2M_i2+(-1)ⁱ⁺³a_i3M_i3 (*)

(разложение по элементам i-й строки.)

Доказательство. Если i=2, то поменяем местами 2-ю и 1-ю строки. Получаем определитель Δ₁,равный —Δ (свойство 2).

Если i=3, то поменяем вначале 3-ю строку со 2-й, а затем

полученную вторую с первой. Получим определитель Δ₂, равный

Δ(свойство 2). Итак,

Аналогично,

.

Замечание. При доказательстве разложения по элементам i-го столбца, предварительно протранспонируем определитель.

Не нашли, что искали? Воспользуйтесь поиском: