Общая теория кривых второго порядка

Удобно будет рассматривать уравнение кривой второго порядка

в следующем виде:

(1)

Сформулируем признаки, позволяющие узнать тип линии по ее уравнению (1).

Введем некоторые определения.

Группу слагаемых a₁₁x²+2а₂₁xy+а₂₂у² назовем группой старших членов. Группу слагаемых 2а₁₃х+2а₂₃у+а₃₃ назовем линейной частью уравнения (1).

Коэффициенты а₁₁, a₁₂, а₂₂ назовем коэффициентами группы старших членов или старшими коэффициентами, а коэффициенты а₁₃, а₂₃, а₃₃ — коэффициентами линейной части или линейными коэффициентами. Отметим, что коэффициент а₃₃ также называется свободным членом уравнения (1).

Осуществим параллельный перенос системы координат ОХY вточку 0'(х₀,у₀), Тогда, как известно, х=х'+х₀, у=у'+у₀ и в новой системе координат уравнение (1) примет вид:

Обозначим коэффициенты при степенях неизвестных в уравнении (*) следующим образом:

(2)

Тогда уравнение (*) примет вид:

(3)

Вывод: при параллельном переносе системы координат, коэффициенты группы старших членов не изменяются, а коэффициенты линейной части изменяются по формулам (2).

Применим формулы поворота системы ОХУ на угол φ т.е.

х=х'соsφ-y'sinφ;

y=x'sinφ+y'cosφ;

Получим:

Тогда в новой системе координат, уравнение (1) примет вид:

где

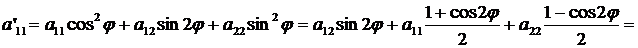
, т.е.

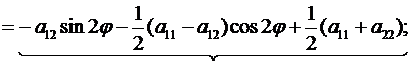
a'₁₃=a₁₃cosφ+a₂₃cosφ

a'₂₃=a₂₃cosφ-a₁₃sinφ (4)

a'₃₃=a₃₃

Вывод: старшие коэффициенты а'₁₁, а'₁₂ и а'₂₂, выражаются только через угол φ старшие коэффициенты а₁₁, а₁₂ и а₂₂. Коэффициенты а'₁₃ и а'₂₃ выражаются только через угол φ и коэффициенты а₁₃, а₂₃. Коэффициенты а'₃₃ и а₃₃ равны.

Для упрощения равенств (4) введем следующие обозначения:

.

Тогда

,

если А 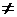0. Введем угол α, где

,

Если же А = 0, то α = 0 и в этом случае a₁₂=(1/2)(а₁₁—а₂₂).

Введем также угол β, считая

, ,

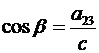если С 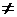0. Если же С=0, т.е. а₁₃=а₂₃=0, то β=0.

Тогда выражения (1.30) перепишутся в виде:

a'₁₁=Азin(2φ+α)+В; а'₁₂=Асоs(2φ+α);

a'₂₂=—Азin(2φ+α)+В; a'₁₃=Csin(φ+β); (5)

a'₂₃= Ссоз(φ+β); а'₃₃=а₃₃.

Отметим, что величины А, В, С и углы α, β не зависят от φ.

Инварианты кривой второго порядка

Инвариантом уравнения (1) относительно преобразования системы координат ОХУ называется такая функция

f(а₁₁, а₁₂, a₂₂, a₁₃, а₂₃, а₃₃),

которая не меняется при переходе к новой системе координат 0'Х'У'. Таким образом, если f — инвариант, то f(a₁₁,...а₃₃) = f(a'₁₁...а'₃₃).

Теорема. Величины

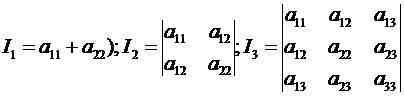(6)

являются инвариантами уравнения (1) линии второго порядка

относительно преобразований декартовой системы координат.

Доказательство проведем вначале для преобразования параллельного переноса, а затем для преобразования поворота.

Инвариантность I₁ и I₂ следует из формул (2). Заметим, что из этих формул также следует, что

(7)

Тогда в новой системе координат O’X’Y’

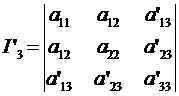
Вычтем из 3-ей строки 1-ю, умноженную на x_0, и затем вторую,

умноженную на у₀. Тогда

Теперь из 3-ro столбца вычтем 1-й, умноженный на x₀ и второй, умноженный на y₀. Получим, что I'₃=I₃.

Рассмотрим теперь преобразование поворота

Разложим I'₃ по элементам 3-го столбца. Получим:

=

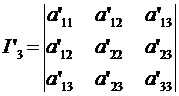(8)

Распишем каждое из 3-х слагаемых в выражении (1.34), пользуясь формулами (1.31).

(9)

(10)

(11)

Следовательно, из (8) следует, что

(12)

Величины А, В, С, углы α, β и I₂ не зависят от угла φ. Значит, при любом повороте системы координат, выражение в правой части (12) не изменяется. С другой стороны, при φ=О, I'₃=I₃. Это и доказывает инвариантность I₃. Теорема доказана.

Определим теперь тип линии в зависимости от знаков инвариантов I₁, I₂ и I₃.

Будем говорить, что

при I₂>О, уравнение (1) задает линию эллиптического типа;

при I₂<О, уравнение (1) задает линии гиперболического типа;

при I₂=О, уравнение (1) задает линии параболического типа.

При параллельном переносе можно попытаться добиться того,

чтобы в уравнении (3) отсутствовали члены 2а'₁₃х' и 2а'₂₃y'. Из формул (2) следует, что это возможно только в том случае, если система

(13)

имеет решение.

Уравнения (13) называются уравнениями центра линии второго порядка. Если х₀, у₀ — решение (13), то точка 0'(х₀,у₀) — центр линии. Если линия имеет центр, то в результате параллельного переноса начала системы координат в точку 0'(х₀,у₀) уравнение линии примет вид

(14)

Поэтому, если точка М(х',у') удовлетворяет уравнению (14), то и точка М'(—х',—у') также удовлетворяет уравнению (14). Таким образом, центр линии является ее центром симметрии.

Заметим, что если кривая второго порядка имеет центр, то, в силу инвариантности I₃, получаем

.

Значит,

(15)

Как было показано ранее, можно повернуть систему координат ОXY таким образом, чтобы уравнение (3) не содержало

члена 2а'₁₂х'у'. Ясно, что в этом случае а'₁₂=0 и из формул (4) следует, что

Следовательно, при а₁₂ 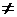0

(16)

Именно при таком выборе угла поворота, уравнение (3) принимает вид:

(17)

Вывод: путем параллельного переноса приводим уравнение кривой к виду (14)

путем поворота, если а₁₂ 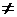О, приводим уравнение (14) к виду:

(17)

в системе координат О"Х"У".

Не нашли, что искали? Воспользуйтесь поиском: