Свойства проецирования

Решение задач основано на знании свойств ортогонального проецирования, представленных в таблице 4.1.

Таблица 4.1 - Свойства ортогонального проецирования

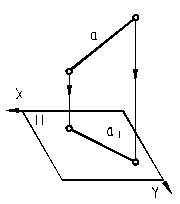
4.1. Проекцией точки является точка.	4.2. Проекцией прямой является прямая (в общем случае).
4.3. Проекцией проецирующей прямой является точка - след прямой (проекция прямой вырождается в точку).	4.4. Проекция точки, лежащей на прямой, лежит на проекции этой прямой.

Продолжение таблицы 4.1

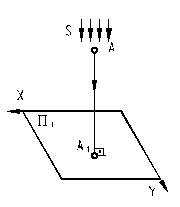
4.5. Проекцией проецирующей плоскости является прямая – след плоскости (проекция плоскости вырождается в прямую).	4.6. Проекция точки, принадлежащая проецирующей плоскости, лежит на следе плоскости.
4.7. Проекция прямой, принадлежащей проецирующей плоскости, совпадает со следом плоскости.	4.8. Проекции параллельных прямых параллельны.

Продолжение таблицы 4.1

4.9. Следы параллельных проецирующих плоскостей параллельны.	4.10. Следы проецирующей плоскости и проекция параллельной ей прямой параллельны.
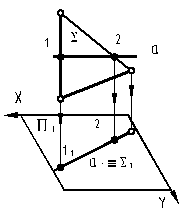
4.11. Следы взаимно перпендикулярных проецирующих плоскостей перпендикулярны друг к другу.	4.12. След проецирующей плоскости и проекция перпендикулярной к ней прямой взаимно перпендикулярны.

Продолжение таблицы 4.1

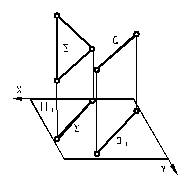
4.13. Проекции отрезка прямой, не параллельного плоскости проекций, меньше самого отрезка прямой, т.к. a1 = a cosa.	4.14. Проекция отрезка, параллельного плоскости проекций, равна самому отрезку (отрезок проецируется в истинную величину).
4.15. Проекции двух взаимно перпендикулярных пересекающихся или скрещивающихся прямых, одна из которых параллельна плоскости проекций, взаимно перпендикулярны.	4.16. Следы двух проецирующих плоскостей образуют угол, равный углу между этими плоскостями.

Продолжение таблицы 4.1

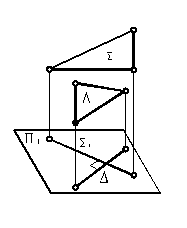
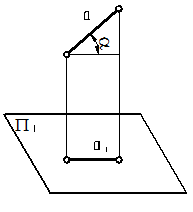
4.17. След проецирующей плоскости и проекции прямой, параллельной плоскости проекций, образуют угол, равный углу между прямой и плоскостью.	4.18. Проекции двух пересекающихся или скрещивающих прямых, каждая из которых параллельна плоскости проекций, образуют угол, равный углу между этими прямыми.
4.19. Проекция любой плоской фигуры, параллельной плоскости проекций, равна самой фигуре.	4.20. Проекция любой выпуклой плоской фигуры является тоже выпуклой.

Не нашли, что искали? Воспользуйтесь поиском: