
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Уравнение неразрывности потока
Гидродинамика
Гидродинамика – это раздел гидравлики, в котором рассматриваются законы движения и взаимодействия жидкости с неподвижными и подвижными поверхностями.
Движение жидкости существенно отличается от движения твердого тела. При движении жидкости расстояние между ее частицами не остается постоянным. Перемещение достаточно малого объема жидкости можно представить в виде суммы трех движений: поступательного, вращательного движения всего объема в целом, а также перемещения различных частиц объема относительно друг друга. В движущейся жидкости учитывают как массовые силы, так и силы трения (вязкость).
Движущаяся жидкость характеризуется двумя параметрами: скоростью течения  и гидродинамическим давлением
и гидродинамическим давлением 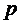 . Основной задачей гидродинамики является определение этих параметров при заданной системе внешних сил.
. Основной задачей гидродинамики является определение этих параметров при заданной системе внешних сил.
Установившимся называется движение, при котором скорость и давление в каждой точке пространства, занятого жидкостью, не изменяются во времени и являются функциями только ее координат:
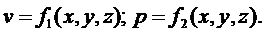
При неустановившемся движении давление 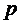 и скорость
и скорость  изменяются в каждой точке не только с изменением координат, но и во времени:
изменяются в каждой точке не только с изменением координат, но и во времени:

Под жидкой частицей в гидродинамике понимают условно выделенный очень малый объем жидкости, изменением формы которого можно пренебречь. Каждая частица жидкости при движении описывает кривую, которая называется траекторией движения.
Под потоком жидкости понимают движущуюся массу жидкости, полностью или частично ограниченную поверхностями. Поверхности раздела могут быть твердыми или образованными самой жидкостью на границе раздела фаз. Границами потоков служат стенки труб, каналов, открытая поверхность жидкости, а также поверхность обтекаемых потоком тел.
Напорным называется движение потока в закрытых руслах при полном заполнении поперечного сечения жидкостью. Например, напорное движение в трубах. Оно возникает за счет разности давлений в начале и конце трубопровода.
Безнапорным называется движение жидкости в открытых руслах, когда поток имеет свободную поверхность. В этом случае движение осуществляется только за счет силы тяжести, т.е. при наличии уклона (движение воды в каналах, реках, лотках и т.п.).
Струи представляют собой потоки жидкости, вытекающие через отверстия или сопла под действием напора. Струи могут быть ограничены со всех сторон газообразной или жидкой средой. В первом случае они называются свободными, во втором – затопленными.

|
Линией тока называют воображаемую кривую в движущемся потоке жидкости, для которой векторы скоростей каждой из частиц жидкости, находящихся на ней в данный момент времени, являются касательными к этой кривой. Линия тока при установившемся движении совпадает с траекторией частиц. Для неустановившегося движения линии тока не совпадают с траекторией. Линия тока характеризует направление движения всех частиц, расположенных на ней в данный момент, а траектория представляет собой путь, пройденной одной частицей за какое-то время 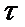 .
.
Если в потоке движущейся жидкости выделить элементарную площадку 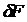 , ограниченную контуром
, ограниченную контуром 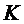 , и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока, а жидкость, движущаяся внутри трубки тока, называется элементарной струйкой. Сечение, расположенное нормально к линиям тока называется живым сечением элементарной струйки.
, и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока, а жидкость, движущаяся внутри трубки тока, называется элементарной струйкой. Сечение, расположенное нормально к линиям тока называется живым сечением элементарной струйки.
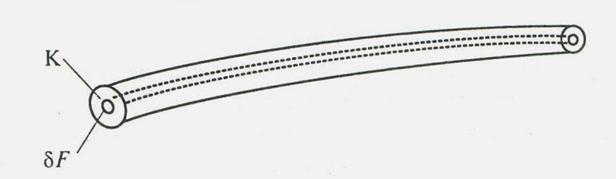
К – контур тока
Элементарная струйка при установившемся движении обладает следующими свойствами:
- ее форма и ориентация в пространстве остаются неизменными по времени;
- боковая поверхность струйки непроницаема для жидкости, т.е. ни одна частичка жидкости не может проникнуть внутрь или выйти наружу через боковые стенки трубки тока;
- ввиду малости живого сечения струйки скорость и давление во всех точках сечения следует считать одинаковыми. Однако вдоль струек значения скорости  и давления
и давления 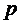 в общем случае могут меняться.
в общем случае могут меняться.
Живым сечением потока F называется площадь сечения, перпендикулярная к направлению линии тока и ограниченная его внешним контуром. Площадь живого сечения потока равна сумме площадей живых сечений элементарных струек.

Смоченным периметром потока П называется длина контура живого сечения, по которому жидкость соприкасается с ограничивающими ее стенками.
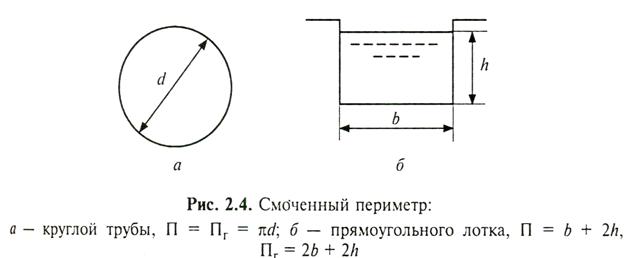
При напорном движении жидкости смоченный периметр П совпадает с геометрическим периметром Пг, при безнапорном не совпадает.
Гидравлическим радиусом R г называется отношение площади живого сечения к смоченному периметру: 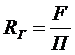
Геометрический радиус и гидравлический радиус – совершенно разные понятия, даже в случае напорного движения жидкости в круглой трубе. Например, для трубы диаметром d геометрический радиус  , а гидравлический
, а гидравлический 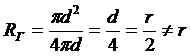 .
.
При гидравлических расчетах часто используется понятие эквивалентного диаметра: 

Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени. Различают объемный Q, массовый M и весовой G расходы жидкости. Они связаны между собой:
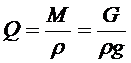
Для элементарной струйки элементарный расход определяется по формуле:

где dF - площадь живого сечения элементарной струйки.
Скорость жидкости в различных точках живого сечения потока различна, и точный закон изменения скорости по сечению не всегда известен, поэтому для упрощения расчетов вводят понятие средней скорости для живого сечения 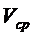 , тогда:
, тогда:  .
.
Средняя скорость – фиктивная скорость потока, которая считается одинаковой для всех частиц данного сечения и подобрана так, что расход, определенный по ее значению, равен истинному значению расхода.
Установившееся движение характеризуется постоянством расхода во времени. Различают равномерное и неравномерное установившееся движение.
Равномерным установившимся движением называется такое движение жидкости, при котором средняя скорость и площади живых сечений потока не изменяются по его длине, например установившееся в цилиндрической трубе, движение в канале призматической формы.

Неравномерным установившемся движением называется такое движение, при котором средняя скорость и площади живых сечений потока изменяются по его длине, например, движение в трубе переменного сечения, движение в открытых руслах при наличии перегораживающего сооружения.
Явления, происходящие в реальных гидравлических устройствах, сложны, поэтому процессы описывают с помощью упрощенных моделей жидкости разной степени идеализации. При необходимости полученные результаты уточняют. В гидродинамике используют четыре модели жидкости:
Þидеальную (невязкую) и несжимаемую, наиболее грубую и простую модель жидкости, когда V=0 и 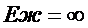 ;
;
Þреальную (вязкую) и несжимаемую, которая учитывает потери энергии на трение и используется при исследованиях статических и энергетических характеристик элементов;
Þидеальную (невязкуго) и сжимаемую, позволяющую с минимальными трудностями рассмотреть динамические процессы в первом приближении;
Þреальную (вязкую) и сжимаемую, наиболее полно отражающую действительность, используемую при детальном исследовании динамических процессов.
Уравнение неразрывности потока
Рассмотрим установившееся движение потока жидкости, ограниченное с боков линиями токов. Двумя произвольными сечениями 1-1 и 2-2, нормальными к линиям тока, выделим некоторый отсек потока.
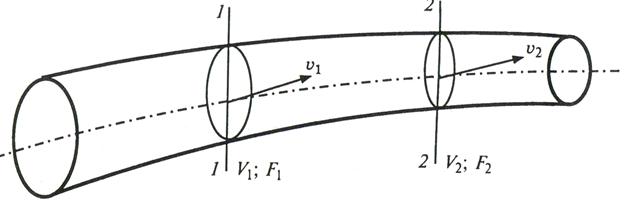
За время  через живое сечение 1-1 внутрь отсека поступает объем жидкости
через живое сечение 1-1 внутрь отсека поступает объем жидкости 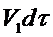 , а через живое сечение 2-2 за то же время из него выходит объем жидкости
, а через живое сечение 2-2 за то же время из него выходит объем жидкости 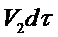 . Учитывая, что проникновение жидкости через боковые поверхности, образованные линиями тока, невозможно, что жидкость несжимаема и соблюдается условие сплошности (т.е. невозможно образование пустот, не заполненных жидкостью), можно утверждать, что объемы жидкости на входе и выходе равны между собой
. Учитывая, что проникновение жидкости через боковые поверхности, образованные линиями тока, невозможно, что жидкость несжимаема и соблюдается условие сплошности (т.е. невозможно образование пустот, не заполненных жидкостью), можно утверждать, что объемы жидкости на входе и выходе равны между собой 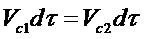 . Поскольку сечения 1-1 и 2-2 взяты произвольно, то можно записать:
. Поскольку сечения 1-1 и 2-2 взяты произвольно, то можно записать:
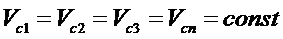
или
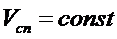 (вдоль потока).
(вдоль потока).
Данное уравнение называют уравнением постоянства расхода или уравнением неразрывности. Оно читается так: при установившемся движении несжимаемой жидкости произведение площади живого сечения на среднюю скорость есть величина постоянная. Его можно записать в следующем виде:
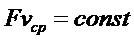 (вдоль потока).
(вдоль потока).
Данное уравнение – первое основное уравнение гидродинамики: при установившемся движении несжимаемой жидкости произведение площади живого сечения  на среднюю скорость
на среднюю скорость 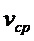 есть величина постоянная. Иначе:
есть величина постоянная. Иначе:
 или
или 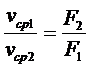 ,
,
т.е. средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.
Уравнение Бернулли
Жидкость, независимо от того, находится ли она в состоянии покоя или движения, обладает некоторым запасом энергии, равной сумме внутренней, потенциальной и кинетической энергии. Внутренняя энергия жидкости представляет собой энергию молекул жидкости, всегда совершающих поступательное и вращательное движение и потому обладающих энергией этих движений.
Рассмотрим сначала случай, когда в жидкости отсутствует вязкое трение (идеальная жидкость) и из числа массовых сил действует только сила тягости.
На рис. 3.2 показан выделенный в потоке идеальной жидкости участок элементарной струйки между сечениями I и 2. Рассмотрим его движение за малое время dt. На левый торец участка струйки площадью dA действует давление p1, на правый торец площадью dA2 -давление p2. Через время dt торцы I и 2, двигаясь со скоростями V1 и V2 , переместятся в положение I’ и 2’ соответственно Работа сил давления и тяжести, приложенных к выделенному объему, равна приращению его кинетической энергии.

| Объем жидкости, заключенный между сечениями 1’ и 2’, в начале и конце движения имеет одно и то же положение и. |
неизменную кинетическую энергию частиц. Поэтому можно рассматривать изменение потенциальной и кинетической энергии только объема, заключенного между I и I/ и как бы переместившегося в пространство между сечениями 2 и 2/.
Учитывая сказанное, приращение кинетической энергии равно 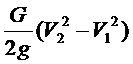 ,
,
где G - сила тяжести крайнего объема:
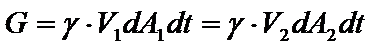
Работа сил тяжести равна 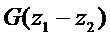 . В результате получаем соотношение
. В результате получаем соотношение

Подставляя выражение для силы тяжести и учитывая уравнение неразрывности потока, 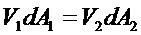 , получаем уравнение Бернулли для потока идеальной жидкости:
, получаем уравнение Бернулли для потока идеальной жидкости:
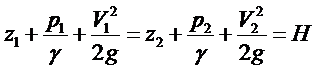
где Н - полный напор в потоке жидкости.
Не нашли, что искали? Воспользуйтесь поиском: