
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема: Анализ временных рядов
Цель работы: изучить методику проведения предварительного анализа временного ряда; научиться выявлять тенденцию во временном ряду; научиться строить аддитивную модель временного ряда; освоить методы проверки адекватности построенной модели; научиться строить прогноз, используя полученную модель.
Общие сведения о временных рядах
Динамические процессы, происходящие в экономических системах, чаще всего проявляются в виде ряда последовательно расположенных в хронологическом порядке значений того или иного показателя, который в своих изменениях отражает ход развития изучаемого явления в экономике. Предварительно рассмотрим ряд понятий.
Последовательность наблюдений одного показателя (признака), упорядоченных в зависимости от последовательно возрастающих или убывающих значений другого показателя (признака), называют динамическим рядом, или рядом динамики. Если в качестве признака, в зависимости от которого происходит упорядочение, выступает время, то такой динамический ряд называется временным рядом.
В данной работе будем рассматривать эконометрические модели, использующие исходные данные, характеризующие один объект за ряд последовательных моментов времени. Время, прошедшее от начального момента наблюдения до конечного, называют длиной временного ряда, а значение показателя в каждый конкретный момент времени - уровнем временного ряда. Обозначим уровни ряда 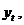 (t =1,2,… n), где n – длина ряда. Временной ряд обычно обозначают Y(t), или
(t =1,2,… n), где n – длина ряда. Временной ряд обычно обозначают Y(t), или  .
.
Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на 3 группы:
1) факторы, формирующие тенденции ряда;
2) факторы, формирующие циклические колебания ряда;
3) случайные факторы.
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы. Если во временном ряду проявляется длительная тенденция изменения экономического показателя, то говорят, что имеет место тренд (рис. 1 а). Обычно эта тенденция описывается с помощью той или иной неслучайной функции T (t) (аргументом которой является t - время), как правило, монотонной. Эту функцию называют функцией тренда или просто – трендом.
Изучаемый показатель может быть подвержен циклическим колебаниям. Среди множества возможных циклических колебаний выделяют сезонные колебания. Эти колебания имеют сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, объем пассажироперевозок, цены на сельхозпродукты) (рис.1 б). Результат действия сезонных факторов обозначим S(t), где S(t) - неслучайная функция. Циклические колебания (конъюнктурные, не сезонные), формируют изменения анализируемого признака, обусловленные действием долговременных циклов экономической или демографической природы (волны Кондратьева, демографические «ямы» и т.п.). Результат действия циклических факторов обозначим С (t), где С (t) - неслучайная функция.
Как правило, временной ряд содержит случайные (нерегулярные), не поддающиеся учету и регистрации колебания. Их воздействие на формирование значений временного ряда как раз и обусловливает стохастическую природу элементов yt, Назовем результат воздействия случайных факторов случайной составляющей и обозначим его через Е (t) или 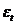 . Элементы случайной составляющей будем называть остатками или ошибками модели.
. Элементы случайной составляющей будем называть остатками или ошибками модели.
Не обязательно, чтобы в процессе формирования значений всякого временного ряда участвовали одновременно факторы всех четырех типов. Однако во всех случаях предполагается наличие случайной составляющей. Некоторые временные ряды не содержат тенденции и циклических компонент, а каждый следующий их уровень образуется под воздействием случайной компоненты (рис. 1 в).
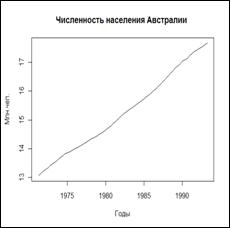
Рис.1.а. Диаграмма временного ряда "Численность населения Австралии, млн.чел." [10] с преобладанием возрастающей тенденции
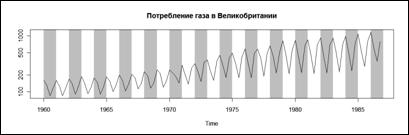
Рис.1. б. Диаграмма временного ряда “ Потребление газа в Великобритании." [10] с преобладанием циклической компоненты

Рис.1. в. Диаграмма временного ряда"Уровень озера Гурон, м" [10] с преобладанием случайной компоненты.
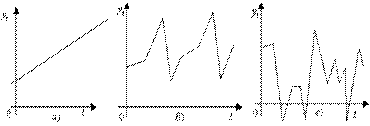
Рис.2. Типичные диаграммы временных рядов [7]
а)- возрастающая тенденция T(t); б) – циклическая S(t); в) – случайная компонента C(t).
Если модель является временным рядом, представленным как сумма трендовой, циклических и случайной компонент, то такая модель называется аддитивной моделью временного ряда.
Общий вид аддитивной модели следующий:
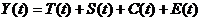
| (1) |
Если в модели временный ряд представлен как произведение перечисленных компонент, то такая модель называется мультипликативной моделью временного ряда.

| (2) |
Основная цель статистического анализа временного ряда заключается в том, чтобы по имеющимся уровням этого ряда построить модель временного ряда для кратко- и среднесрочного прогноза.
Для достижения указанной цели необходимо решить следующие задачи:
1) провести предварительный анализ данных;
2) определить, какие из неслучайных компонент  ,
,  или
или 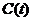 присутствуют в формировании временного ряда;
присутствуют в формировании временного ряда;
3) построить модели для тех неслучайных компонент, которые присутствуют в разложениях (1) или (2);
4) провести проверку адекватности моделей;
5) подобрать модель, адекватно описывающую поведение случайных остатков  и статистически оценить параметры этой модели.
и статистически оценить параметры этой модели.
6) провести расчет точечного и интервального прогнозов.
Показатели временного ряда
Для статического анализа одномерных временных рядов вида: y1,у2,…уn вычисляют ряд показателей:
- первые разности или абсолютный цепной прирост 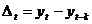 , который показывает величину изменения показателя за k интервалов времени;
, который показывает величину изменения показателя за k интервалов времени;
- вторые разности или абсолютное ускорение  , которое показывает величину изменения абсолютного цепного прироста за k интервалов времени;
, которое показывает величину изменения абсолютного цепного прироста за k интервалов времени;
- средний абсолютный прирост: 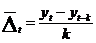 т.е. прирост в единицу времени;
т.е. прирост в единицу времени;
-коэффициент роста для t-го периода: 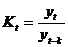
-коэффициент прироста  .
.
На практике также часто применяют показатель темпа роста и темпа прироста:
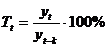 , где
, где 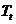 -темп роста для t -го периода;
-темп роста для t -го периода;
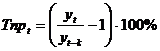 где
где 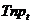 - темп прироста для t -го периода.
- темп прироста для t -го периода.
Приведенные формулы чаще всего применяют при k =1.
Важной характеристикой временного ряда является также средний уровень ряда: 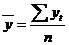 , где n длина ряда.
, где n длина ряда.
В табл.1. приведены формулы расчета показателей
Таблица 1
Не нашли, что искали? Воспользуйтесь поиском: