Аддитивная и мультипликативная модели временного ряда

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели выражается соотношением (1) будем полагать, что циклическая компонента отсутствует, т.е.:

,

(20)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой ,сезонной и случайной компонент.

Уравнение (2) показывает общий вид мультипликативной модели в предположении, что циклическая компонента отсутствует, уравнение примет вид:

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой , сезонной и случайной компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний изменяется, то строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений компонент , и для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты .

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных 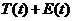в аддитивной или в мультипликативной модели.

4) Аналитическое выравнивание уровне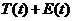й или и расчет значений с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений или .

6) Расчет значений остатков выполняется по формуле 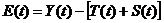или 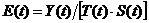. Если полученные значения остатков не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

Основная идея расчета значений сезонной компоненты заключается в нахождении разности между средними значениями за каждый предполагаемый период и общим средним за весь период наблюдений. При этом следует помнить, что общее среднее значение сезонной составляющей равно нулю.

Методику построения каждой из моделей рассмотрим ниже на примере.

Оценка качества построенных моделей

Модель считается хорошей со статистической точки зрения, если она адекватна и достаточно точна.

Проверка адекватности модели реальному явлению является важным этапом прогнозирования социально - экономических процессов. Для этого исследуют ряд остатков 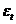, которые вычисляются по формуле

,

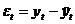(21)

Т.о., 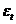характеризует расхождение между фактическим уровнем ряда и -теоретическим, рассчитанным с помощью модели, в момент времени t. Поскольку 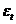рассчитываются для каждого момента времени (t =1,2,… n), то они образуют ряд остатков, который также принято называть остаточной компонентой.

Наиболее важными свойствами остаточной компоненты являются:

§ равенство математического ожидания уровней ряда остатков нулю;

§ независимость уровней ряда остатков,

§ случайность уровней ряда остатков;

§ соответствиенормальномузаконураспределения уровней ряда остатков.

Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы 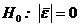. С этой целью строится t- статистика:

,

(22)

(3.4.22)

где - среднее арифметическое значение уровней ряда остатков :

,

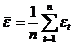(22)

-среднеквадратическое отклонение для этой последовательности, .

Если , то гипотеза H₀ принимается, в противном случае принимается альтернативная гипотеза , где – определяется с помощью распределения Стьюдента с учетом уровня значимости и числа степеней свободы 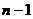. Если гипотеза H₀ отвергается, то модель считается неадекватной

Проверка условия случайности возникновения отдельных отклонений от тренда.

Для проверки случайности уровней ряда могут быть использованы критерий серий и критерий поворотных точек.

Критерий “восходящих” и “нисходящих” серий был описан ранее в разделе определение наличия тренда.

Критерий «пиков» или критерий поворотных точек. Значение случайной переменной считается поворотной точкой, если оно одновременно больше (меньше) соседних с ним элементов. В случайной выборке математическое ожидание числа точек поворота р и дисперсия выражаются формулами:

; ,

(24)

Т.е. если остатки случайны, то поворотная точка приходится примерно на каждые 1,5 наблюдения.

Критерием случайности с доверительной вероятностью 95%, является выполнение неравенства

,

где р – фактическое количество поворотных точек в случайном ряду; 1,96 – квантиль нормального распределения N (0,1) при уровне значимости равном 5%. Квадратные скобки здесь означают, что от результата вычисления следует взять целую часть.

Этот критерий случайности отклонений от тренда при 5%-ном уровне значимости можно представить как

(25)

Если неравенство не соблюдается, то ряд остатков нельзя считать случайным (т.е. он содержит регулярную компоненту) и, стало быть, модель не является адекватной.

Не нашли, что искали? Воспользуйтесь поиском: